Ток проводимости и ток смещения.

Ток смещения или абсорбционный ток — понятие из области теории классической электродинамики. Введено Дж. К. Максвеллом при построении теории электромагнитного поля для описания слабых токов, возникающих при смещении заряженных частиц в диэлектриках. Величину, равную скорости изменения во времени (t) электрической индукции D (точнее, величину (∂D/∂t)/4π), Максвелл назвал Т. с.

Электрический ток проводимости - как явление - направленное движение свободных носителей электрического заряда в веществе или в вакууме.

Сумма тока проводимости и тока смещения называется полным током.

Линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости. Если они не замкнуты, замыкаются токами смещения.

Уравнения Максвелла в интегральной и дифференциальной форме, физический смысл каждого уравнения.

Полную систему уравнений Максвелла в интегральной форме составляют приведенные ниже уравнения (5.6.1) – (5.6.2).

Первое уравнение является обобщением закона электромагнитной индукции. Оно имеет следующий вид

. (5.6.1)

Интеграл по зк (E,dl)= - интеграл по S(dB/dt, dS)

Это уравнение означает, что циркуляция напряженности E электрического поля по произвольному замкнутому контуру L , мысленно проведенному в электромагнитном поле, равна взятому с обратным знаком потоку вектора через поверхность S, ограниченную этим контуром. Иными словами с переменным магнитным полем связано индуцированное вихревое электрическое поле. Причем это электрическое поле существует, не зависимо от того, находится в нем проводник или нет.

Второе уравнение Максвелла

(5.6.2)

Интеграл по зк (H,dl)= интеграл по S(j+dD/dt, dS)

означает, что циркуляция напряженности H магнитного поля по произвольному неподвижному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна полному току через поверхность S, ограниченную этим контуром. Полный ток равен сумме тока проводимости I=интергал по S(j,dS) и тока смещения Iсм=интергал по S(dD/dt , dS). Из этого уравнения следует, что даже в отсутствие тока электрических зарядов возникает индуцированное магнитное поле, связанное с переменным электрическим полем.

Третье уравнение является обобщением электростатической теоремы Гаусса. Оно имеет вид

, (5.6.3)

Интеграл по зк (D,ds)= интеграл по V(r,dV)

где r – объемная плотность свободных зарядов. Это уравнение означает, что поток электрической индукции (электрического смещения) D через произвольную неподвижную замкнутую поверхность S, мысленно проведенную в электромагнитном поле, равен суммарному свободному заряду в объеме V, ограниченном этой поверхностью.

Четвертое уравнение

(5.6.4)

Интеграл по зк (B,dS)= 0

означает, что поток магнитной индукции B, через произвольную неподвижную замкнутую поверхность S, мысленно проведенную в электромагнитном поле, равен нулю.

Величины, входящие в уравнения Максвелла, связаны дополнительными соотношениями (материальными уравнениями), которые учитывают реакцию среды на электромагнитное поле. Для изотропной не сегнетоэлектрической и не ферромагнитной среды эти уравнения имеют вид

; (5.6.5)

; (5.6.6)

. (5.6.7)

С помощью известных из векторного анализа теорем Стокса и Гаусса можно представить полную систему уравнений Максвелла в дифференциальной (локальной) форме:

; ротор E=-dB/dt (5.6.10)

; ротор H=j+dD/dt (5.6.11)

; дивергенция D=r (5.6.12)

. дивергенция B=0 (5.6.13)

На границе раздела сред производные, входящие в уравнения (5.6.10) – (5.6.13), вообще говоря, не определены. В этом случае необходимо пользоваться граничными условиями для электромагнитного поля, вытекающими из уравнений Максвелла в интегральной форме:

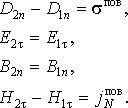
D2n-D1n=sпов

E2t=E1t

B2n=B1n

H2t-H1t=jпов (5.6.14)

Здесь используются следующие обозначения:

sпов – поверхностная плотность свободных зарядов в точке М на границе раздела двух сред, около которой определяются проекции векторов;

n – единичный вектор нормали к поверхности раздела сред, проведенный из среды 1 в среду 2;

t – единичный вектор, касательный к поверхности раздела;

N=[n,t] – единичный вектор, касательный к поверхности раздела и ортогональный t;

jпов – вектор линейной плотности поверхностного тока проводимости.

Вектор jпов направлен вдоль поверхности по направлению тока в ней и численно равен , где dIпов – сила тока проводимости, проходящего через малый участок длиной dl сечения поверхности, проведенного перпендикулярно направлению поверхностного тока.

При заданных значениях e, m, s, sпов и jпов и известных E(x,y,z) и H(x,y,z) в начальный момент времени t=0 система дифференциальных уравнений Максвелла (5.6.10) – (5.6.13) имеет единственное решение.

Если электрическое и магнитное поля стационарны, т.е. частные производные D и B равны нулю , то, как следует из уравнений (5.6.10) – (5.6.13), эти поля существуют независимо друг от друга. В этом случае электрическое поле описывается двумя основными уравнениями электростатики:

. ротор Е=0,div D=r (5.6.15)

Соответственно магнитное поле описывается двумя основными уравнениями магнитостатики:

. rotH=j,divB=0 (5.6.16)