1.4 Линии напряжённости электрического поля

П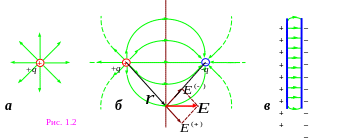 оле можно попробовать представить наглядно, рисуя в каждой точке пространства векторы напряжённости поля от каждого точечного заряда-источника (или малого элемента протяжённого заряженного тела), а затем их складывая. Очевидно, такая процедура, хотя принципиально всегда и осуществима, но практически весьма долгая и утомительная даже в случае поля всего двух точечных зарядов. Пример такой деятельности представлен на рис. 1.2. Там же проведены и так называемые «силовые линии» (или «линии напряжённости») – линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряжённости в данной точке. Они помогают представить структуру электрического поля – его направление и величину в разных точках пространства. О величине судят при этом по «густоте» силовых линий в данной области пространства, т. е. по их количеству, отнесённому к площади «пронзаемой» поверхности. Скоро мы уточним это понятие.

Майкл Фарадей, которому и принадлежит идея использования силовых линий, предложил быстрый способ складывать множество векторов. Он предложил строить картину силовых линий экспериментально, используя огромное количество мелких диэлектрических частичек-стрелок, которые ориентируются в каждой точке пространства вдоль вектора («по полю») быстро и «самостоятельно».

На рис. 1.2 приведены картины силовых линий поля одиночного точечного заряда – a (для положительного они направлены радиально от заряда); двух разноимённых б, одинаковых по модулю зарядов; поля между двумя плоскопараллельными разноимённо заряженными пластинами – в. В последнем случае вдали от краёв этих пластин мы имеем дело с т. н. однородным полем. Электрическое поле называется однородным, если его напряжённость одинакова во всех точках пространства. Силовые линии однородного поля – равноотстоящие друг от друга параллельные прямые.

• Сделаем несколько важных замечаний о силовых линиях электростатического поля

1. Силовые линии электростатического поля незамкнуты! Такое поле порождено источниками – электрическими зарядами – они начинаются на положительных и заканчиваются на отрицательных зарядах.

2. Линии напряжённости непрерывны и не пересекаются.

3. Как мы уже отмечали, величина напряжённости поля пропорциональна густоте силовых линий в данной области пространства. В случае поля одиночного точечного заряда силовые линии отражают не только качественно верную картину структуры поля, но и точное количественное соответствие теории – густота линий уменьшается по мере удаления от заряда-источника поля обратно пропорционально квадрату расстояния от него!

1.5 Применение принципа суперпозиции для нахождения напряжённости поля системы зарядов и протяжённых заряженных тел

Мы уже отмечали, что введённая нами величина – напряжённость электрического поля будет плодотворной, если мы научимся рассчитывать её по заданному распределению заряженных частиц и тел в пространстве. Первым способом такого расчёта является использование знания выражения для напряжённости поля точечного заряда и принципа суперпозиции электрических полей. По сути, его мы и используем (пусть и качественно) при «теоретическом» построении картины силовых линий, описанном в предыдущем пункте. Такой способ принципиально применим всегда. Другое дело, что получить точный результат аналитически, без применения численных методов и ЭВМ, удаётся только в очень ограниченном ряде случаев распределения зарядов-источников в пространстве. Приведём только простейший пример такого расчёта. Ведь наша задача сейчас продемонстрировать «стратегию» действий, а не углубляться в математические «упражнения». Примеры рассмотрения более сложных ситуаций вы найдёте в нашем учебном пособии для семинарских занятий.

Пример. Определить напряжённость электрического поля на оси равномерно заряженного кольца радиуса R. Заряд кольца q, x – расстояние от центра кольца.

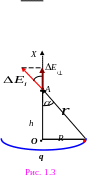
Прежде всего разобьём кольцо на элементы – точечные заряды q_i, каждый из которых создаёт в точке А поле с напряжённостью

.

О братим внимание, что расстояние от элемента кольца до точки А одинаково для всех таких элементов. Все векторы располагаются под одинаковым углом  к оси ОХ на конической поверхности (см. рис. 1.3).

Д

q_i

алее воспользуемся принципом суперпозиции, т.е. сложим все такие векторы. Вследствие симметрии задачи вклад в общую напряжённость дадут лишь составляющие напряжённости  Е_ix. Поэтому модуль вектора напряжённости в точке А будет определятся только суммой этих составляющих Е_ix по всем элементам кольца:

.
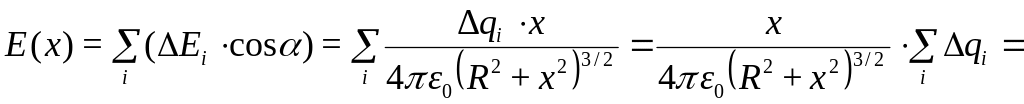