6.2 Закон Ома для неоднородного (содержащего эдс) участка цепи

Закон Ома для участка цепи с ЭДС связывает силу постоянного тока, протекающего по участку, разность потенциалов на его концах ₁₂ и действующую на участке ЭДС . За время t по участку переносится заряд равный q = It . Электрическое поле и сторонние силы, действующие на участке, совершают работу:

. (*)

На участке цепи выделяется при этом тепло:

. (**)

Если на участке цепи проводники не движутся, а значит, не совершается механическая работа, то эти величины можно приравнять. После сокращения на q получим

или

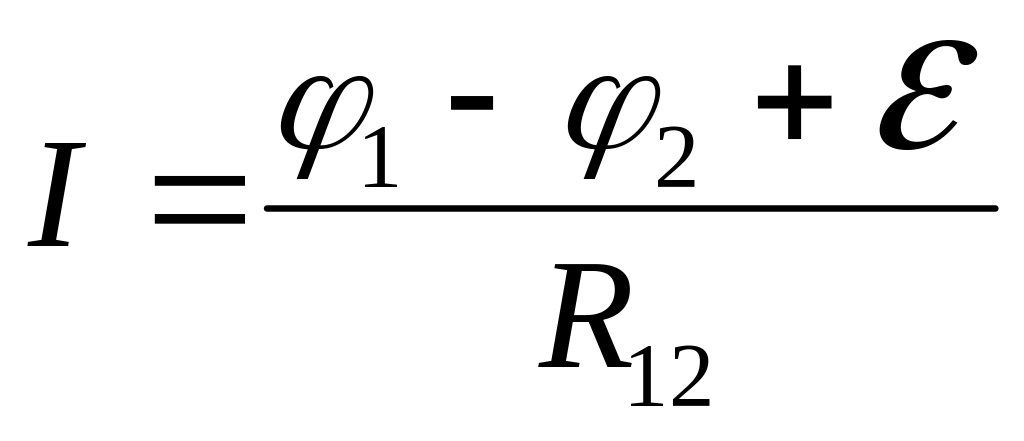. (6.2)

Это и есть закон Ома для неоднородного (содержащего ЭДС) участка цепи. Сделаем к нему ряд важных замечаний.

Важные замечания

1. В соотношении (6.2) I и ₁₂ – следует понимать как алгебраические величины, т.е. имеющие определённый знак. При движении вдоль участка от точки 1 к точке 2 знаки силы тока I и д 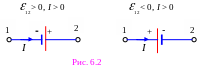ействующую на участке ЭДС ₁₂ выбираются положительными, если направление тока и ЭДС источника совпадают с направлением обхода. При этом считается, что ЭДС направлена от отрицательного полюса источника тока к положительному (в направлении повышения потенциала положительных зарядов – сторонние силы совершают положительную работу). Рисунок 6.2 иллюстрирует правило знаков.

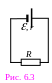2. В отсутствии сторонних сил на участке цепи (источников тока) мы естественным образом приходим к уже знакомому закону Ома для однородного участка:

.

3. Если же точки 1 и 2 – концы неоднородного участка цепи замкнуть, то получится так называемая «полная цепь»: источник тока с ЭДС  и внутренним сопротивлением r, подключенный соединительными проводами к участку внешней цепи с сопротивлением R – см. рис. 6.3. В этом случае выполняется закон Ома для полной цепи:

• Сила тока, протекающего в полной цепи, равна отношению ЭДС источника тока к полному сопротивлению этой цепи (к сумме сопротивлений внешнего и внутреннего её участков):

. (6.3)

4. Несколько формально мы использовали некую характеристику участка цепи R₁₂ – его «полное сопротивление», ответственное за выделение тепла Джоуля-Ленца. Если выделить из этой величины омическое сопротивление однородных участков (не входящих в источник тока) R, то останется так называемое «внутреннее сопротивление» источника тока:

_{r = R12 – R. (6.3)}

_{К ак же узнать внутреннее сопротивление источника тока на практике? Для этого надо замкнуть перемычкой полюса источника и измерить так называемый «ток короткого замыкания Iк.з.» – см рис. 6.4. Тогда внутреннее сопротивление источника можно будет найти так:}

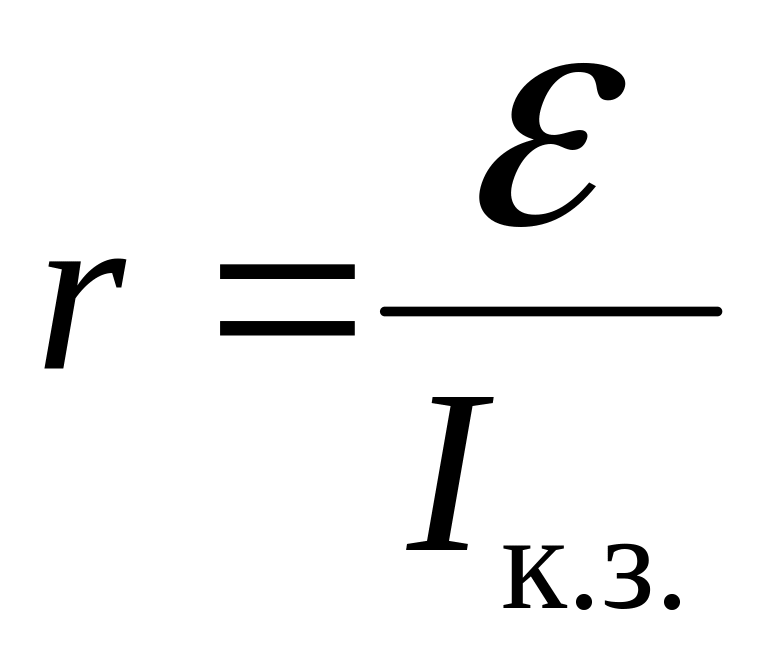. (6.4)

5. Ещё одно замечание касается терминологии. Произведение силы тока на сопротивление R часто называют «падением напряжения» на однородном участке. Но лучше, во избежание путаницы, не пользоваться этим термином! Дело в том, что произведение силы тока на полное сопротивление неоднородного участка цепи определяет «электрическое напряжение» на этом участке: .

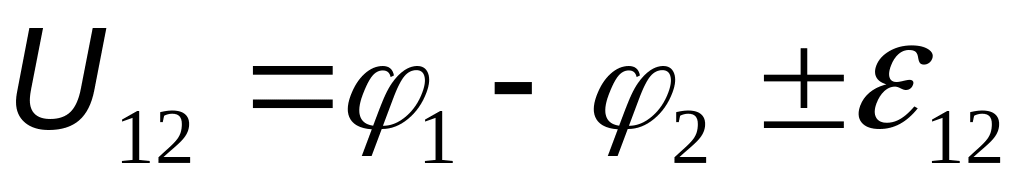   • Дополнение Рассмотрим пример, помогающий понять, как применяется закон Ома для неоднородного участка. Рассмотрим участок разветвлённой цепи постоянного тока между точками 1 с потенциалом ₁ и точкой 2 с потенциалом ₂ (см. рис. 6.5). Пусть ток протекает по участку от точки 1 к точке 2. Построим график изменения потенциала  вдоль участка цепи между этими точками. В направлении протекающего тока потенциал сначала на однородном участке с сопротивлением R₁ равномерно^*) уменьшается от точки 1 до отрицательного полюса источника тока. Падение потенциала по закону Ома для однородного участка цепи составляет IR₁. Будем предполагать, что на участке включён «химический» источник тока. Тогда при переходе от его отрицательной пластины к электролиту потенциал увеличивается скачком на величину его электрохимического потенциала. Второй скачок потенциала вверх происходит при переходе от электролита к положительной пластине источника. Внутри же источника тока ток протекает по проводящему веществу – электролиту, и потенциал опять-таки уменьшается на величину Ir, как и на любом однородном участке цепи. Аналогично потенциал уменьшается равномерно на однородном участке между положительным полюсом источника и точкой 2 на величину IR₂, достигая конечного значения потенциала – ₂. В нашем примере мы получили, что он оказался больше, чем потенциал ₁ (см. рис. 6.5) – т.е. ток течёт в направлении повышения потенциала в цепи. Вот и ответ на вопрос: «Может ли ток по участку цепи протекать от точки с меньшим потенциалом к точке с большим?». Может, если на участке действуют сторонние силы с ЭДС большей, чем падение потенциала на полном сопротивлении участка.

Приведённый анализ поведения потенциала помогает проиллюстрировать ответ на ещё один важный вопрос: «Что покажет вольтметр, подключенный к полюсам источника тока?». Если вольтметр считать идеальным, то он измерит разность потенциалов между этими полюсами (точками a и b на рисунке). Его показания в рассмотренном случае (направление тока через источник совпадает с направлением его ЭДС) будут равны:

U_v = ₂ – Ir. (6.5)

Если бы ток проткал по участку 1–2 в противоположном направлении, то показания вольтметра были бы иными:

U_v = ₂ + Ir. (6.6)

О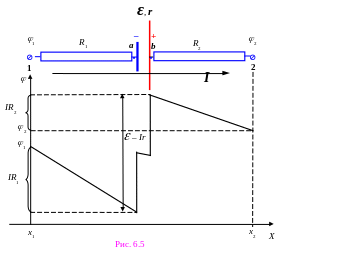 боснуйте этот результат самостоятельно, построив график зависимости потенциала вдоль участка цепи для такого случая. Эта ситуация реализуется, в частности, при зарядке аккумуляторов – ток через источник протекает против направления его ЭДС через (от положительного полюса к отрицательному).