§6.Теоремы о среднем. Возрастание и убывание функции

Если функция непрерывна на отрезке дифференцируема хотя бы на интервале и , то существует такая точка , что (т. Ролля).

Если функция непрерывна на отрезке и дифференцируема хотя бы на интервале , то существует такая точка , что .(т.Лагранжа)

Если на промежутке производная функции больше (меньше) нуля, то функция на этом промежутке возрастает (убывает), если ровна нулю, то .

30. Доказать теорему: Если уравнение имеет положительный корень , то уравнение также имеет положительный корень и притом меньший .

.

31. . Выяснить, сколько действительных корней имеет уравнение 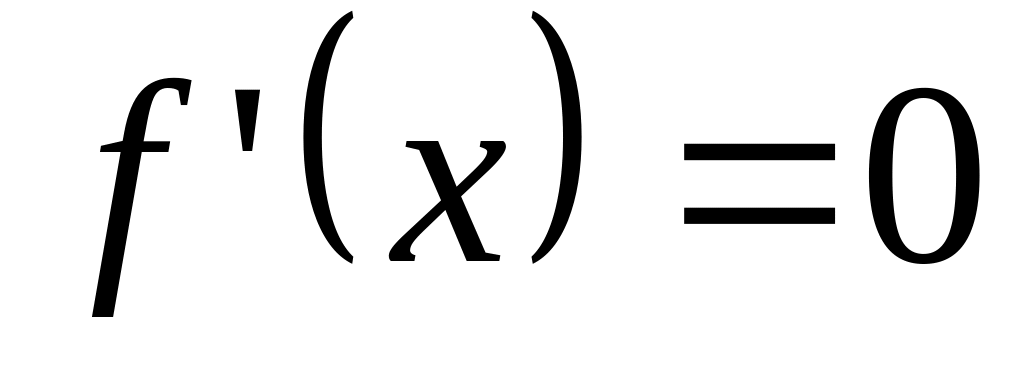и указать интервалы, в которых они лежат.

Функция на отрезках удовлетворяет условиям теоремы Роля, следовательно, на интервалах будут находиться корни уравнения , а так как уравнение третьей степени не может иметь больше трех корней, то других корней нет.

32. Доказать тождество: .

Рассмотрим функцию : , следовательно, на всей числовой оси , а так как при , то при всех .

33. Доказать неравенство: .

Рассмотрим функцию . На любом отрезке она непрерывна и дифференцируема, следовательно, выполняется формула Лагранжа , так как убывает, то при имеем , а при имеем , таким образом, при всех .

34. Показать, что функция убывает в интервале .

. В промежутке между корнями , а это значит, что на функция убывает.

35. Найти интервалы монотонности функций:

    1. .

при , то есть при и

при и

Таким образом, функция возрастает при , ; функция убывает при , .

2. .

,

при .

36. Доказать справедливость неравенства: .

Рассмотрим функцию . При , следовательно, функция возрастает, то есть для всех , то есть , что равносильно неравенству . при , следовательно, функция убывает, то есть для всех , а это значит .

37. Докажите, что уравнение имеет действительный корень и только один.

38. Докажите справедливость неравенств:

    ;

    .

39. Доказать неравенства:

;	;
;	.

§7.Правило Лопиталя

Если при , стремящемуся к конечному или бесконечному пределу , функции и одновременно стремятся к нулю или бесконечности, то при условии, что предел существует.

40. Найти пределы функций:

    1. ;

    2. ;

    3. 

.

41. Найти пределы функций:

;	;	;
;	;	;
;	.
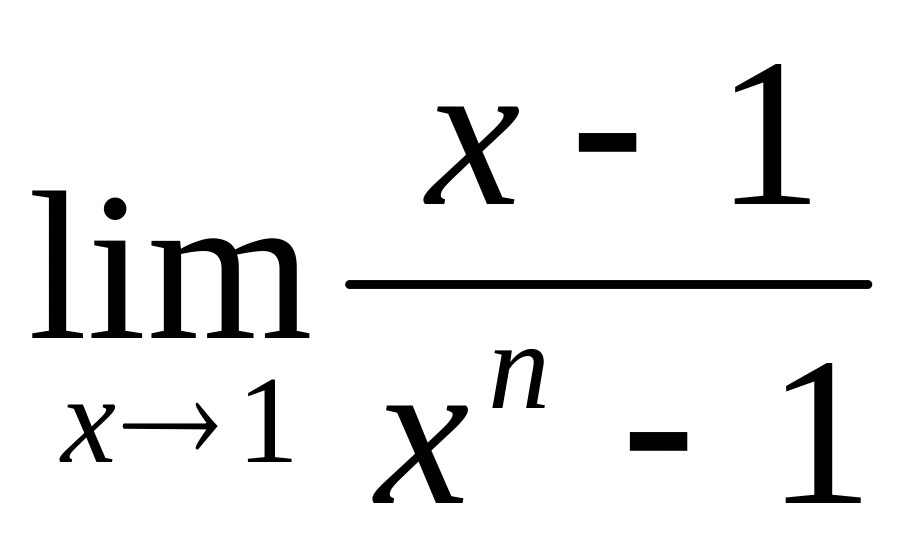
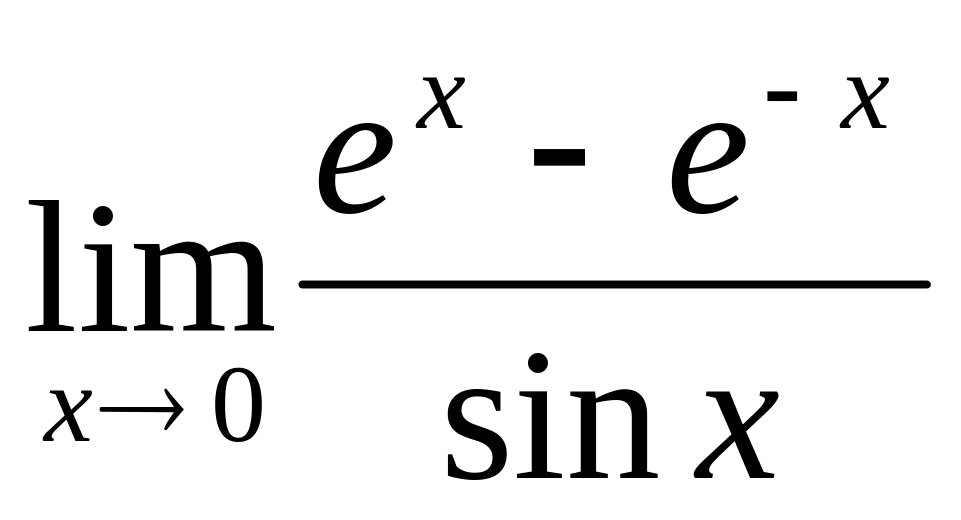
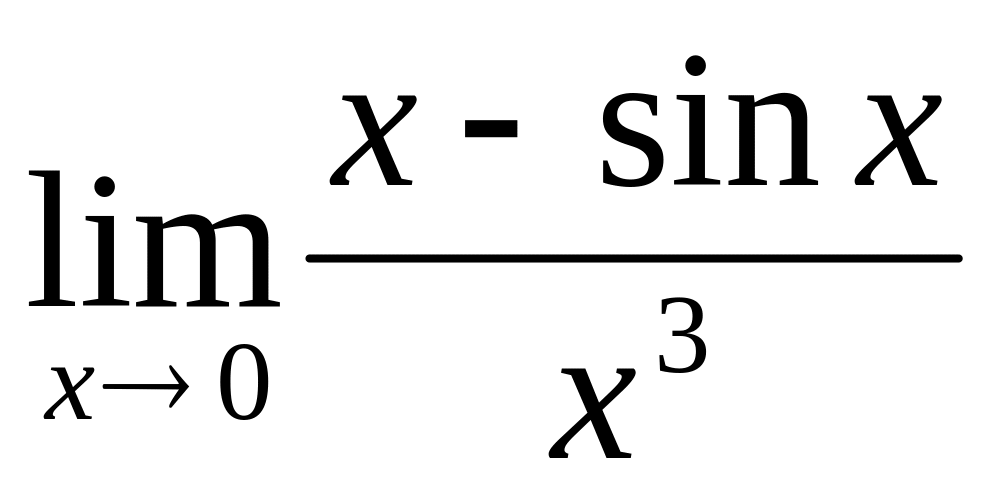