§1.Определение производной

Пусть – внутренняя точка , .

1. Исходя из определения, найти производные функций:

   1. 

Функция определена на всей числовой оси. Возьмем произвольное и придадим ему произвольное приращение , найдем соответствующее приращение и найдем предел их отношения:

.

Вычислим значение производной в точке .

2. .

   1. ;

   2. ;

   3. 

.

.

3. 

   1. ;

   2. ;

   3. .

.

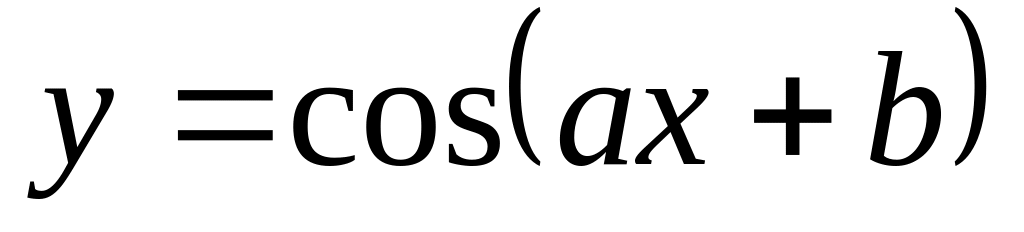§2.Техника дифференцирования

Таблица производных:

;	;	;
;	;	;
;	;	;
;	;	;
;	.

Правила дифференцирования:

;	;
;	.

2. Продифференцировать следующие функции:

   1. 

.

2. .

.

3. .

.

4. .

.

5. .

.

6. .

.

7. .

.

3. Продифференцировать следующие функции:

	;
;	;
;	;
;	;
;	;
;	;
;	;
;	;
;	.

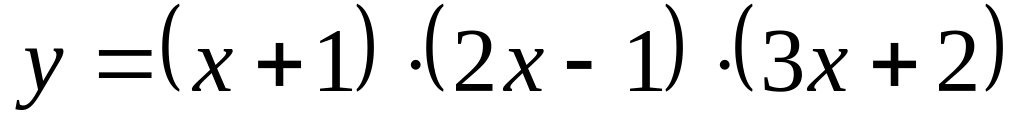§3.Дифференциал

Функция называется дифференцируемой в точке , если ее приращение в данной точке может быть представлено в виде: . Главная часть этого представления называется дифференциалом функции в точке , .

Необходимым и достаточным условием дифференцируемости функции одной переменной является существование производной этой функции в данной точке, причем , то есть .

4. Используя определение дифференцируемой функции, доказать, что функция дифференцируема на всей числовой оси.

Пусть – произвольная точка оси, придадим приращение и найдем соответствующее приращение функции

;

.

5. Используя определение дифференцируемости функции, доказать, что функция не дифференцируема в точке , .

Перейдем из точки в точку и найдем соответствующее приращение функции . Приращение функции не удалось представить в виде , следовательно, функция в точке не дифференцируема.

6. Найти дифференциалы следующих функций:

   1. . .

   2. .

.

3. . .

1. Зная, что , найти приближенно .

. Положим , так как .

..

8. Найти приближенное значение .

9. Исходя из определения доказать, что

   1. дифференцируема на всей числовой оси;

   2. не дифференцируема в точке .

10. Найти приращение и дифференциал функции в точке при . Указать величину приращения и дифференциал функции на чертеже.

11. Найти дифференциалы следующих функций:

    ;

    .

12. Найти приближенные значения:

;

;

.