6.3 Метод прогонки

Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:

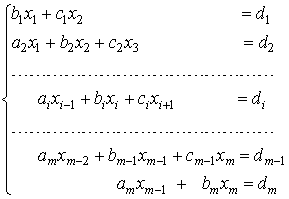
Преобразуем первое уравнение системы к виду , где: , . Подставим полученное выражение во второе уравнение системы и преобразуем его к виду: и т.д.

На i-ом шаге уравнение преобразуется к виду: , где , .

На m-ом шаге подстановка в последнее уравнение выражения

дает возможность определить значение :

.

Значения остальных неизвестных находятся по формулам:

, i = m-1, m-2, ..., 1.

ПРИМЕР 4. Решение системы методом прогонки.

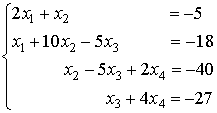
Прямой ход прогонки. Вычислим прогоночные коэффициенты:

, ,

,   

, ,

,

Обратный ход прогонки. Находим значения неизвестных:

, , ,

Ответ:

      .

Задание для самостоятельной работы

1. Методом Гаусса с выбором главного элемента найти решение системы уравнений: .

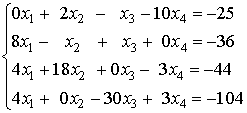2. Найти 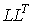  разложение матрицы:

.

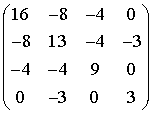3. Можно ли применять метод Холецкого к системе уравнений, матрица которой имеет вид:

.

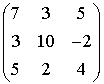4. Подсчитать количество арифметических действий в методе прогонки.

Вопросы

1. Что такое прямые и итерационные методы.

2. С какой целью применяют модификацию метода Гаусса - схему частичного выбора.

3. Для каких систем уравнений применяют метод Холецкого.

4. Запишите формулы для нахождения решения после приведения системы к виду.

5. Сформулируйте алгоритм метода прогонки.

7 Решение систем линейных алгебраических уравнений итерационными методами

Рассматривается система Ax = b. Для применения итерационных методов система должна быть приведена к эквивалентному виду x=Bx+d. Затем выбирается начальное приближение к решению системы уравнений и находится последовательность приближений к корню. Для сходимости итерационного процесса достаточно, чтобы было выполнено условие

.

Критерий окончания итераций зависит от применяемого итерационного метода.

7.1 Метод Якоби

Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное x₁, из второго уравнения системы выразим x₂, и т. д. В результате получим систему уравнений с матрицей, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:

  , i, j = 1, 2, ... n.

Компоненты вектора d вычисляются по формулам:

  , i = 1, 2, ... n.

Расчетная формула метода простой итерации имеет вид:

,

или в покоординатной форме записи выглядит так:

,  i = 1, 2, ... m.

Критерий окончания итераций в методе Якоби имеет вид:

, где    .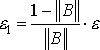

Если , то можно применять более простой критерий: окончания итераций

ПРИМЕР 1. Решение системы линейных уравнений методом Якоби.

Пусть дана система уравнений:

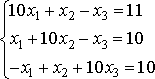
Требуется найти решение системы с точностью   

Приведем систему к виду удобному для итерации: .

Выберем начальное приближение, например, 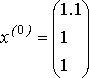- вектор правой части.

Тогда первая итерация получается так:

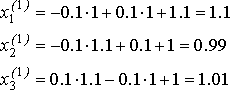
Аналогично получаются следующие приближения к решению.

, ,

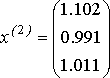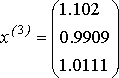Найдем норму матрицы .  Будем использовать норму .

Так как сумма модулей элементов в каждой строке равна 0.2, то = 0.2 < 1/2, поэтому критерий окончания итераций в этой задаче .

Вычислим нормы разностей векторов:   ,  .

Так как  , заданная точность достигнута на четвертой итерации.

Ответ: x ₁ = 1.102, x ₂ = 0.991, x ₃ = 1.101