24. Методика изучения основных соотношений в окружности. Вписанные и описанные многоугольники.

Понятие самой окружности и её элементов дается в 7 классе.

Определение: окружностью с центром в точке и радиусом называется геометрическая фигура, состоящая из всех точек плоскости, находящихся на расстоянии от точки плоскости.

Далее дается обозначение окружности и перечисляются 3 возможные случая взаимного расположения прямой и окружности:

1. не имеют общих точек

2. имеют только 2 общие точки

3. имеют только 1 общую точку.

Определение: прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Далее в 9 классе в теме описанные и вписанные многоугольники эта тема рассматривается более подробно.

Если прямая имеет 2 общие точки с окружностью, то она называется секущей.

Взаимное расположение окружности и прямой характеризуется соотношением между расстоянием от центра окружности до прямой и радиусом окружности:

1. Прямая имеет только 2 общие точки с окружностью, если расстояние от центра окружности до прямой меньше радиуса окружности.

2. Прямая имеет только 1 общую точку с окружностью, если расстояние от центра окружности до прямой равно радиусу окружности.

3. Прямая не имеет общих точек с окружностью, если расстояние от центра окружности до прямой больше радиуса окружности.

Все это приводится с доказательствами.

Более подробно рассматривается случай касания прямой и окружности:

Касательной к окружности называется прямая, имеющая единственную общую точку с окружностью.

Единственная общая точка называется точкой касания.

Теорема (свойство касательной): касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.

Понятие отрезков касательной.

2 Следствия:

1. Отрезки касательных к окружности, проведенные из одной точки, равны.

2. Отрезки касательных к окружности, проведенные из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Теорема (признак касательной): прямая, проходящая через точку окружности и перпендикулярная ее радиусу, проведенному в эту точку, касается окружности.

Далее рассматривается взаимное расположение 2 окружностей:

1. Окружности не имеют общих точек (не пересекаются).

2. Окружности имеют две общие точки (пересекаются).

3. Окружности имеют одну общую точку и одна из них лежит внутри круга, ограниченного другой окружностью (касаются внутренним образом).

4. Окружности имеют одну общую точку и одна из окружностей не лежит внутри круга, ограниченного другой окружностью (касаются внешним образом).

Теорема1 (свойство окружностей, касающихся внешним образом) Если две окружности касаются внешним образом, то расстояние между их центрами равно сумме их радиусов.

Теорема2 (условие касания окружностей внешним образом) Если расстояние между центрами двух окружностей равно сумме их радиусов, то такие окружности касаются внешним образом.

Теорема3 (условие касания окружностей внутренним образом) Две окружности касаются внутренним образом тогда и только тогда, когда расстояние между их центрами равно модулю разности их радиусов.

Дуга окружности называется полуокружностью, если её концы служат концами диаметра этой окружности.

Дуга окружности и центральный угол, внутри которого лежит эта дуга, называется соответствующими.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который меньше развернутого, то эта дуга меньше полуокружности.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который больше развернутого, то эта дуга больше полуокружности.

Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла.

Две дуги одной и той же окружности называются равными, если равны их градусные меры.

Вписанным углом в окружность называется угол, вершина которого лежит на окружности, а обе его стороны пересекают окружность.

Теорема (о вписанном угле): Градусная мера вписанного угла равна половине меры дуги, на которую он опирается.

Следствия:

1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2. В писанный угол, опирающийся на полуокружность, прямой.

Теорема 2 (об угле между хордой и касательной). Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.

Угол, образованный двумя хордами и опирающийся на них, и  центральный угол связаны соотношением .

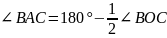Определение: окружностью с центром в точке и радиусом называется геометрическая фигура, состоящая из всех точек плоскости, находящихся на расстоянии от точки плоскости.

Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом окружности.

Отрезок, соединяющий две точки окружности, называется ее хордой.

Хорда, проходящая через центр окружности, называется ее диаметром.

Если на окружности взять две точки, то они разобьют окружность на две части, каждая из которых называется дугой окружности.

Определение: прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Если прямая имеет две общие точки с окружностью, то она называется секущей.

Соотношения между прямыми и отрезками окружности

Пропорциональные линии в круге Если две хорды АВ и CD пересекаются внутри круга в точке Е, то произведение отрезков одной хорды равно произведению отрезков другой хорды, т. е. AЕ·ЕВ = DE·EC
Если из точки, взятой вне окружности, проведены две секущие АС и AC1, то справедливо равенство AB·AC=АВ1·АС1.
Теорема о квадрате касательной Если из точки, лежащей вне круга, проведены секущая MB и касательная МС, то справедливо равенство МC 2 = МВ·МА

О трезки касательных, проведенных из одной точки, равны: AB = AC

Углы между прямыми и отрезками окружности

Угол между пересекающимися хордами	Угол между касательными		Угол между касательной и хордой
Угол между секущими, пересекающимися вне окружности		Угол между касательной и секущей

Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Медиана - отрезок, соединяющий вершину с серединой противолежащей стороны.

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, которая содержит противолежащую сторону треугольника

Биссектриса - отрезок биссектрисы угла , соединяющий вершину с точкой противолежащей стороны.

Серединный перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Внешний угол – угол, смежный с каким-нибудь углом треугольника.

Соотношения между углами и сторонами треугольника:

1. Сумма углов в треугольнике равна 180.

2. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

3. В треугольнике против большей стороны лежит больший угол.

4. В треугольнике против большего угла лежит большя сторона.

Неравенство треугольника:

Каждая сторона треугольника меньше суммы двух других его сторон.

Следствия:

1) Для любых 3 точек, не лежащих на одной прямой, справедливо неравенство . 2)Каждая сторона больше разности двух других его сторон.

Т.(о свойстве биссектрисы ): Биссектриса делит противолежащую сторону в таком отношении, в каком находятся прилежащие стороны.

Т.(о точке пересечения медиан ): Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

Т.(о выражении площади через стороны и синус угла между ними):Площадь равна половине произведения длин двух его сторон на синус угла между ними.

Т.(синусов): Стороны пропорциональны синусам противолежащих углов.

Т.(косинусов): квадрат любой стороны равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

Понятие изучается в 7 классе, а также его основные элементы и признаки равенства треугольников. Виды треугольников, сумма углов треугольника, неровенство треугольника и признаки равенства прямоугольных треугольников.

В 8 классе изучается признаки подобия треугольников и соотношения между сторонами и углами прямоугольного треугольника(синус, косинус, тангенс и котангенс), площадь треугольника(площадь треугольника равна половине произведения длины стороны на высоту, проведенную к ней).

9 класс: замечательные точки , вписанные и описанные треугольники, теорема синусов и косинусов, площадь треугольника (Площадь равна половине произведения длин двух его сторон на

1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

2. Медианы треугольника делят его на равновеликие треугольники. Треугольники называются равновеликими, если у них равны площади.

3. Точку пересечения медиан треугольника называют центром тяжести или центром масс.

Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, которая содержит противолежащую сторону треугольника

Теорема.: Прямые, на которых лежат высоты , пересекаются в одной точке (ортоцентр).

Теорема (о свойстве биссектрисы угла): Каждая точка биссектрисы угла, меньше развернутого, равноудалена от его сторон. Каждая точка указанного угла, равноудалена от его сторон, лежит на биссектрисе этого угла.+док

Теорема.(о точке пересечения биссектрис): Биссектрисы треугольника пересекаются в одной точке.

Точка пересечения биссектрис является центром вписанной окружности.

Теорема.: Серединные перпендикуляры к сторонам пересекаются в одной точке.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром описанной окружности. Точка пересечения серединных перпендикуляров в остроугольном треугольнике лежит внутри треугольника, в прямоугольном - на середине гипотенузы, а в тупоугольном - вне треугольника.

Внешний угол – угол, смежный с каким-нибудь углом треугольника.

Средние линии - это отрезки, соединяющие середины двух сторон. Поэтому для построения средней линии необходимо выполнить следующие действия: 1) найти середины двух сторон треугольника; 2) соединить середины сторон отрезком - это и будет средняя линия.

Три средние линии треугольника образуют "вписанный" в него , называемый серединным. Его площадь в четыре раза меньше площади данного .

Точка пересечения медиан, биссектрис и высот треугольника наз. замечательными точками . Данная тема изучается в 9 классе.

Сначала рассматриваются треугольники, а затем четырехугольники.

Определение: четырехугольник называется вписанным в окружность, если окружность проходит через все его вершины.

Теорема: около четырехугольника можно описать окружность (четырехугольник вписать в окружность) тогда и только тогда, когда сумма его противоположных углов равна 180⁰ .

Теорема 1. Сумма противоположных углов вписанного четырёхугольника равна180°.

Пусть в окружность с центром О вписан четырёхугольник ABCD (черт. 412). Требуется доказать, что  /  А + /  С = 180° и /  В + /  D = 180°.

/    А, как вписанный в окружность О, измеряется  ¹/₂  BCD.

/   С, как вписанный в ту же окружность, измеряется  ¹/₂  BAD.

Следовательно, сумма углов А и С измеряется полусуммой дуг BCD и BAD в сумме же эти дуги составляют окружность, т. е. имеют  360°.  Отсюда  /   А + /   С = 360° : 2 = 180°.

Аналогично доказывается, что и 

/   В + /   D = 180°. Однако это можно вывести и иным путём. Мы знаем, что сумма внутренних углов выпуклого четырёхугольника равна 360°. Сумма углов А и С равна 180°, значит, на сумму других двух углов четырёхугольника остаётся тоже 180° .

Определение: четырехугольник называется описанным около окружности, если окружность касается всех его сторон.

Теорема: в выпуклый четырёхугольник можно вписать окружность (около окружности описать четырехугольник) тогда и только тогда, когда сумма длин его противоположенных сторон равны.