12. Методыка вывучэння тоесных пераўтварэнняў выразаў у школьным курсе матэматыкі

Тождественное преобразование не является отдельной темой школьного курса математики. Они изучаются на протяжении всего курса алгебры и начал анализа. На основе тождественных преобразований у школьников формируются представления об аналитических методах математики. Так как решение каждой математической задачи аналитическим методом как правило требует выполнение тождественных преобразований.

Целью тождественных преобразований (Т.П) может быть приведение выражению вида, более удобного для численных расчетов или дальнейших преобразований.

К Т.П относятся: приведение подобных членов, раскрытие скобок, разложение на множители, приведение алгебраических дробей к общему знаменателю, избавление от иррациональности в знаменателе и т.п.

Для успешного осуществления Т.П. целых А.В нужно помнить: Формулы сокращенного умножения, Свойства степени с целыми показателями, Формулы корней квадратного трехчлена ax2 + bx + c, Теорему Виета х1 и х2 — корни ax2 + bx + с, Разложение квадратного трехчлена ax2 + bx + c на множители.

О введении понятии тождества:

В различных учебниках алгебры применяются различные определения тождества:

1. Равенство, верное при любых значения переменных: (x+1)² =x²+2x+1

2. Равенство, верное при всех допустимых значениях переменных: ОДЗ: x≥3

3. Равенство, верное при любых значениях переменных, принадлежащих данному множеству:

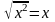• - тождество на множестве x≥0

• x²-2x+2=0 – тождество напустом множестве

Схема введения тождества:

1. рассматриваются свойства действий над числами: для любых чисел а, б и с имеют место переместительный, распределительный и сочетательный свойства

2. дается определение тождественно равных выражений: два выражения называются тождественно равными, если при всех значениях переменной их соответствующие значения равны. Это определение предваряется рассмотрением выражения x(y+7) и xy+7x и вычисление их значений при x=9 и y= -2, показывает, что эти значения равны. И далее говорится, что из переместительного и распределительного следует, что соответствующие значения этих выражений равны при любых значениях переменных

3. дается определение тождественного преобразования, как замены одного выражения другим тождественно равным ему выражением

4. рассматриваются соответственные упражнения на закрепление:

• почему все соответствующие значения выражений р+25 и 25+р равны ?

• запишите два тождественно равных выражения, содержащих одну, две, три переменных

• доказать, что выражение с(с-3) и с²-3 не являются тождественно равными

наконец приводится определение понятия тождества

Тождеством называется равенство верное при любых значениях переменных.

Позже в следующем классе при рассмотрении рациональных дробей тождество определяется как равенство верное при всех допустимых значений входящих в него переменных (таким образом понятие тождество в школьном курсе дается в развитии).

Рассмотрим примеры мотивировок (целей) тождественных преобразований:

1. тождественные преобразования 3,45х – 3,45у = 3,45(х - у), удобно мотивировать тем, что упрощается нахождение числового значения выражения 3,45х – 3,45у (вместо трех действий выполняется два) ;

2. выполняя тождественное преобразование: х³ – х² – 2х + 2 = (х - 1)(х² – 2), можно отметить, что его целесообразно применять, когда решается уравнение х³ – х² – 2х + 2 = 0;

3. свойство возрастания функции f(x)=(x-1)/x легко обнаруживается после тождественного преобразования (x-1)/x = 1-1/x;

4. с целью получения более простого выражения:

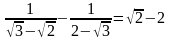
Другие приемы повышения эффективности изучения тождественных преобразований.

При изучении тождественных преобразований начинающий учитель часто испытывает затруднения в поддержании интереса школьников в активизации их мыслительной деятельности, в развитии наблюдения, догадки.

Одним из эффективных приемов повышения интереса учащихся в этом плане является отыскание различных способов решения.

Например: сократите дробь

1. 

2. 

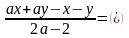
Среди приемов, способствующих сознательному усвоению учащимися тождественных преобразований на раннем этапе усвоения обычно является следующее:

1. проведение аналогии между тождествами и числовыми выражениями: – (а + в) = - а – в

проверим на числах: – (5 + 3) = - 8

- 5 – 3 = -8

-8 = -8 значит – (5 + 3) = - 5 – 3

2. теоретическое обоснование:

– (а + в) = - а – в

– (а + в) = -1(а + в) = (-1)а + (-1)в = -а - в

3. варьирование:

под варьированием понимается прием, позволяющий взглянуть на данное преобразование с разных сторон в разных конкретных ситуациях. Например, при ознакомлении учащихся с тождеством – (а + в) = - а – в полезно прочитать и записать его не только слева направо, но и наоборот: - а – в = – (а + в).

Смысл этих записей различный: первое обозначает тождественное преобразование по внесению знака в скобку, а второе – по вынесению знака за скобку. Возможны и другие вариации данного тождества, а именно: - (- а – в) = а+в и наоборот а – в = - ( -а + в)