Глава 4. Численные методы (процедуры) минимизации функции одной переменной

В связи с тем, что градиент функции многих переменных указывает направление наискорейшего возрастания функции в окрестности точки, в которой вычисляется градиент, то поиск минимума функции многих переменных по существу сводится к минимизации функции одной переменной.

4.1. Постановка задачи.

Пусть R={x:- <x<} - числовая ось, X - некоторое множество из R, f(x) - функция, определённая на множестве X и принимающая во всех точках xX конечные значения. Примерами множеств X из R являются: отрезок, интервал, полуинтервалы. Будем рассматривать задачу минимизации функции f(x) на множестве X.

Определение 1: Точку x_*X называют точкой минимума функции f(x) на множестве X, если f(x_*)f(x) для всех xX; величину f(x_*) называют наименьшим или минимальным значением f(x) на X и обозначают . Множество всех точек минимума f(x) на X будем обозначать через X_* .

В зависимости от свойств множества X и функции f(x) множество X* может содержать одну, несколько или даже бесконечно много точек, а также возможны случаи, когда X* пусто.

Пример 1: Пусть при x0 и f(0)=0. На множестве X={x: 1 x  2} минимальное значение F(x) равно нулю, множество X_* содержит одну точку x_* =1. Если X={x: 1/3  x 1}, то множество X_* содержит три точки: 1/3, 1/2, 1; если X={x: 0  x  1}, то X_* = {x: x =1/n, n=1,2,…} - счётное множество. В случае, когда X={x: 2 x < } функция f(x) не имеет наименьшего значения на X. В самом деле, какую бы точку xX ни взять, найдётся точка yX (например, y = k при достаточно большом k), такая что f(x)>f(y). Это значит, что X_* = .

Пример 2: Функция на X={x: x1} принимает своё наименьшее значение, равное нулю, во всех точках отрезка X_* ={x: 0 x1}. Если X={x: 1  x  2}, то X_* содержит одну точку x_*=1; если X={x: 1 < x  2}, то X_* = .

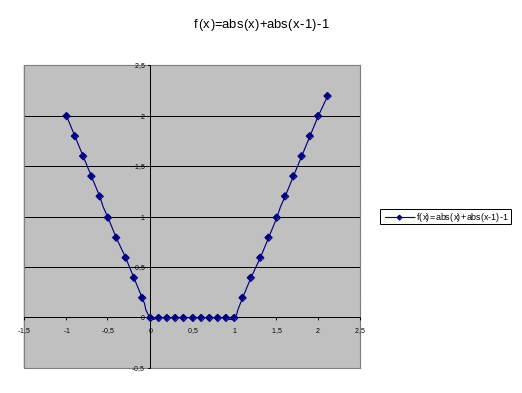
Пример 3: Пусть f(x)=x при x0 и f(0)=1. На множествах X={x: 0  x  1} или X={x: 0 < x  1} эта функция не имеет наименьшего значения, т.е. X_* =.

Пример 4: Пусть f(x) = ln(u), X={x: 0 < x  1}. Здесь X_* =, так как во всех точках из X функция принимает конечные значения, а для последовательности x_k =1/k, (k=1,2,…) имеем .

Определение 2: Функция f(x) называется ограниченной снизу на множестве X, если существует такое число М, что f(x)М для всех xX. Функция F(x) не ограничена снизу на X, если существует последовательность {x_k}X, для которой .

В примерах 1-3 функции ограничены снизу на рассматриваемых множествах, а в примере 4 функция не ограничена.

В тех случаях, когда X_* =, естественным обобщением понятия наименьшего значения функции является понятие нижней грани функции.

Определение 3: Пусть функция f(x) ограничена снизу на множестве X. Тогда число f_* называют нижней гранью f(x) на X, если

1. f_*  f(x) при всех xX;

2. для любого сколь угодно малого числа >0 найдётся точка x_X, для которой f(x_)<f_* + . Если функция f(x) не ограничена снизу на X, то в качестве нижней грани F(x) на X принимается f_* =-. Нижнюю грань f(x) на X обозначают через .

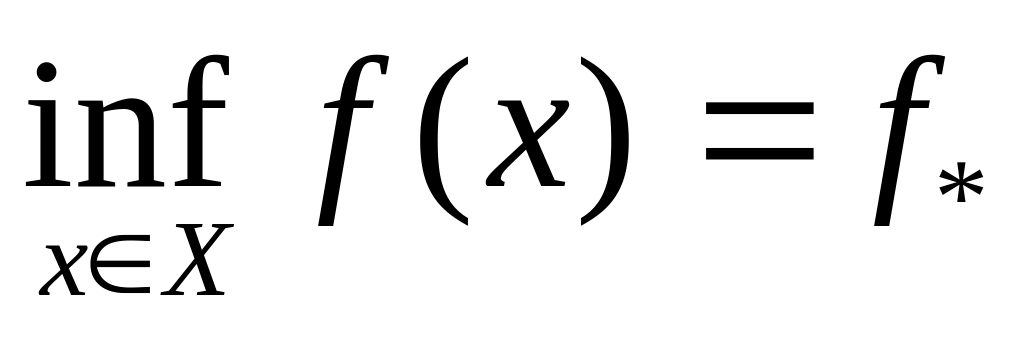В примерах 1-3 нижняя грань J_* =0, а в примере 4 f_* =-.

Если X_* , то очевидно, нижняя грань f(x) на X совпадает с наименьшим значением этой функции на X, т.е. В этом случае говорят, что функция f(x) на X достигает своей нижней грани. Подчеркнём, что всегда существует, а , как мы видели из примеров 1-4, не всегда имеет смысл. Введём ещё два определения.

Определение 4: Последовательность {x_k}X называется минимизирующей для функции f(x) на множестве X, если

.

Из определения и существования нижней грани следует, что минимизирующая последовательность всегда существует.

Определение 5: : Скажем, что последовательность {x_k} сходится к непустому множеству X, если , где - расстояние от точки x_k до множества X.

Теорема К. Вейерштрасса. Всякая непрерывная функция на замкнутом ограниченном множестве достигает экстремума (минимума, максимума).