
- •1. Дифференцируемость функции в точке. Правила дифференцирования. Таблица производных.
- •2. Основные теоремы о дифференцируемых функциях. Правило Лопиталя.
- •3. Производные высших порядков. Дифференциал. Дифференциалы высших порядков.
- •4. Формула Тейлора и ее остаточный член.
- •5. Исследование функций одной переменной. Монотонность, точки экстремума.
- •6. Исследование функций одной переменной. Направление выпуклости, точки перегиба, асимптоты.
- •7. Первообразная и неопределенный интеграл. Таблица неопределенных интегралов.
- •8. Замена переменных в неопределенном интеграле. Интегрирования по частям.
- •9. Интегральные суммы и определенный интеграл. Условия интегрируемости функций. Геометрический смысл определенного интеграла.
- •10. Классы интегрируемых функций. Свойства определенного интеграла.
- •11. Интеграл с переменным верхним пределом.
- •12. Замена переменных в опред.Интеграле. Интегрирование по частям
- •13. Опреднление вещественного линейного пространства. Примеры
- •14. Линейная зависимость и независимость векторов
- •15. Базис и размерность линейных пространств. Базис n-мерных векторных пространств.
- •16. Базис n-мерных векторных пространств. Координаты вектора
- •17. Преобразования координат
- •18. Линейные отображения и линейные операторы. Примеры линейных отображений и линейных операторов
- •19. Матрица линейного оператора
- •20. Действия над линейными операторами.
- •21. Преобразование матрицы линейного оператора при переходе к новому базису.
- •22. Собственные векторы и собственные значения линейного оператора. Характеристическая матрица и характеристический многочлен.
- •23. Векторное пространство . Расстояние в . Топологические понятия. Последовательности в .
- •24. Понятие функции n переменных. Предел функции n переменных.
- •25. Непрерывность функции n переменных. Основные определения и теоремы.
- •26. Дифференцируемость функции n переменных. Частные производные. Производная по направлению. Градиент.
- •27. Безусловный и условный экстремумы функций двух переменных.
- •28. Площадь фигуры и объем тела.
- •29. Определение двойного интеграла по прямоугольной и произвольной областях.
- •30. Свойства двойного интеграла.
- •31. Сведение двойного интеграла к повторному
- •32. Преобразование фигуры и замена переменной в двойном интеграле. Использование полярных координат.
- •33. Тройной интеграл: определение и свойства. Сведение тройного интеграла к повторному.
- •34. Криволинейный интеграл первого рода. Определение, вычисление и свойства.
- •1. Линейность.
- •35. Определение криволинейного интеграла второго рода и его вычисление
- •36. Свойства криволинейного интеграла второго и его вычисление.
- •37. Формула Грина. Условие Эйлера.
- •38. Числовые ряды. Положительные ряды. Гармонический и геометрический ряды.
- •39. Признаки сравнения для положительных рядов. Признаки Даламбера и Коши.
- •40. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.
- •41. Функциональные последовательности и функциональные ряды. Основные определения.
- •42. Степенные ряды. Теорема Абеля. Радиус сходимости. Ряд Тейлора.
21. Преобразование матрицы линейного оператора при переходе к новому базису.
Пусть f – линейный оператор пространства Vn, а A и B – его матрицы соответственно в базисах
E = (e1, e2, . . . , en) (12.10)
EƘ = (e’1, e’2, . . . , e'n).
Пусть
вектор x
линейного пространства Vn
имеет координатный столбец X
=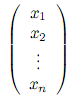 в
базисе (12.10) и координатный столбец X’
=
в
базисе (12.10) и координатный столбец X’
=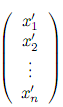 в
базисе (12.11). Пусть далее вектор y = f(x),
который является образом вектора x при
отображении f, имеет координатный столбец
Y =
в
базисе (12.11). Пусть далее вектор y = f(x),
который является образом вектора x при
отображении f, имеет координатный столбец
Y =
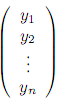 в
базисе (12.10), а в базисе (12.11) – Y ‘
=
в
базисе (12.10), а в базисе (12.11) – Y ‘
=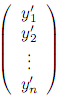 ->
Y
= AX, (12.12) Y ‘
= BX'.
->
Y
= AX, (12.12) Y ‘
= BX'.
С другой стороны, учитывая, что S-матрица перехода от базиса (12.10) к базису (12.11)
X = SX’, (12.14)
Y = SY’. (12.15)
Умножив равенство (12.14) слева на матрицу A, получим AX = ASX’ или учитывая (12.12) и (12.15), получаем
SY’ = ASX’. Отсюда Y’ = S−1ASX’. Сравнивая последнее равенство с (12.13), имеем B = S−1AS. (12.16)
Таким образом, если матрица A – матрица оператора f в базисе (12.10), а S – матрица перехода от базиса (12.10) к базису (12.11), то матрица B оператора f в базисе (12.11) может быть найдена из соотношения (12.16).
Верно обратное. Пусть A – матрица линейного оператора f в базисе (12.10), S – произвольная невырожденная матрица и такая, что B = S−1AS. Если (12.11) – такой базис пространства Vn, что S – матрица перехода от (12.10) к (12.11), то в силу формулы (12.16) матрица B – матрица оператора f в базисе (12.11).
Отсюда получаем теорему.
Теорема 12.5. Две квадратные матрицы A и B n-го порядка тогда и только тогда являются матрицами некоторого линейного оператора f пространства Vn, когда существует невырожденная матрица S n-го порядка, такая, что выполняется равенство B = S−1AS.
Следствие 12.5.1. Если линейный оператор имеет в некотором базисе невырожденную матрицу, то и в любом другом базисе матрица этого оператора является невырожденной.
22. Собственные векторы и собственные значения линейного оператора. Характеристическая матрица и характеристический многочлен.
Ненулевой вектор u ∈ Vn называется собственным вектором линейного оператора f, если существует число λ∈P такое, что выполняется равенство f(u) = λu.
Число λ называется собственным значением (собственным числом) оператора f.
Множество всех собственных значений оператора f называется спектром этого оператора.
Свойства собственных векторов
Свойство 1. Каждому собственному вектору линейного оператора соответствует единственное собственное значение.
Свойство 2. Если u – собственный вектор линейного оператора f с собственным значением λ и α – любое отличное от нуля число, то αu – также собственный вектор оператора f с собственным значением λ.
Д о к а з а т е л ь с т в о. Так как f(u) = λu, то отсюда следует, что f(αu) = αf(u) = αλu = λ(αu).
Свойство 3. Если u1,u2 собственные векторы линейного оператора f с одним и тем же собственным значением λ,тоu1+u2 –либо нулевой вектор либо также собственный вектор этого оператора с собственным значением λ.
Свойство 4. Собственные векторы линейного оператора, соответствующие разным собственным значениям, линейно независимы.
Линейный оператор в пространстве Vn называется оператором простой структуры, если в пространстве Vn существует базис из собственных векторов этого оператора.
Теорема 12.9 (критерий оператора простой структуры). Линейный оператор f пространства Vn является оператором простой структуры тогда и только тогда, когда в некотором базисе этого пространства матрица оператора f является диагональной.
Матрица (A − λEn) называется характеристической матрицей линейного оператора f (матрицы A).
Многочлен ϕ(λ) = det(A − λEn) называется характеристическим многочленом оператора f (характеристическим многочленом матрицы A). Иногда характеристическим многочленом называют многочлен ϕ(λ)=det(λEn − A).
Уравнение det(A − λEn) = 0 называется характеристическим уравнением оператора f (характеристическим уравнением матрицы A). Корни характеристического уравнения над множеством C (C – множество комплексных чисел) называются характеристическими числами оператора f (матрицы A).
Свойство 1. Характеристический многочлен полураспавшейся матрицы равен произведению характеристических многочленов ее диагональных клеток.
Свойство 2. Характеристические многочлены подобных матриц равны.
