6. Исследование функций одной переменной. Направление выпуклости, точки перегиба, асимптоты.
Пусть y=f(x) определена и непрерывна на (а,в). Если на интервале (а,в) график ф-ции расположен выше секущей, проходящей через точка у(а) и у(в), то говорят, что на интервале (а,в) ф-ция y=f(x) выпукла вверх.
Если же график ф-ции расположен ниже секущей, то говорят, что на интервале (а,в) ф-ция y=f(x) выпукла вниз.
Если ф-ция y=f(x) определяется в точке х0 и при переходе через эту точку ф-ция y=f(x) меняет направление выпуклости, то говорят, что х0 – точка перегиба.
Асимптоты
Наклонные асимптоты.
Прямую y = kx+b называют правосторонней наклонной асимптотой функции f(x), если f(x) = kx+b+λ(х) при x→+∞.
Прямую y = kx + b называют левосторонней наклонной асимптотой функции f(x), если f(x) = kx+b+λ(х) при x→−∞.
Вертикальные асимптоты.
Пусть функция f(x) непрерывна на (a,c) и существует левосторонний предел f(c − 0), равный +∞ или −∞. Тогда прямую x = c называют левосторонней вертикальной асимптотой. Аналогично, если f(x) непрерывна на (c,b) и существует левосторонний предел f(c + 0), равный +∞ или −∞, то прямую x=c называют правосторонней вертикальной асимптотой.
7. Первообразная и неопределенный интеграл. Таблица неопределенных интегралов.
Функция F(x) называется первообразной для функции f(x) на множестве X, если F’(x) = f(x) для любого x ∈ X.
Неопределенный
интеграл – это множество первообразных.
где F(x) - одна из первообразных, C -
произвольная постоянная.
Линейностью
интеграла
называют свойство, выраженное формулой
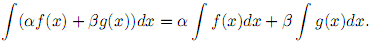
Таблица первообразных
8. Замена переменных в неопределенном интеграле. Интегрирования по частям.
Внесение
множителя под знак дифференциала.
Пусть v = v(x) дифференцируемая на X функция,
такая, что f(x) представима в виде
Тогда
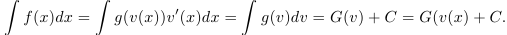
Линейная
подстановка.
Частным случаем введения множителя под
знак дифференциала является линейная
подстановка. а=/0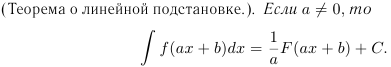
Вынесение
множителя из-под знака дифференциала.
Пусть функция x = x(t) дифференцируема на
промежутке T, x’(t)
=/
0, и значения x заполняют X. Тогда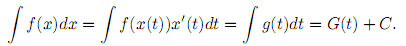
Интегрирование по частям.
Теорема.
Пусть u(x) и v(x) - дифференцируемые функции,
определенные на X. Если
имеет
первообразную на X, то и
также
имеет первообразную на X, причем
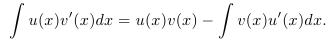
Формулу
называют формулой
интегрирования по частям
неопределенного интеграла.
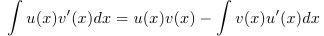
Коротко
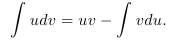
9. Интегральные суммы и определенный интеграл. Условия интегрируемости функций. Геометрический смысл определенного интеграла.
Разбиением отрезка [a,b] будем называть всякое конечное, упорядоченное по возрастанию множество точек X = {x0, x1, ..., xn} отрезка [a, b ] таких, что x0 = a, xn=b, т.е. X = {xk|a = x0<x1<...<xk−1<xk<...<xn=b}.
Диаметром разбиения X называют число δ(X)=max{xk−xk−1},δ(X)>0.
Разбиение делит отрезок [a, b ] на части [xk−1, xk ], k = 1, 2, ..., n , причем
Длину отрезка [xk−1, xk] будем обозначать ∆xk: ∆xk=xk−xk−1
Пусть X = {x0, x1, ..., xn} — разбиение отрезка [a, b ]. На каждой части [xk−1, xk ] произвольным образом возьмем промежуточную точку ξk ∈ [xk−1,xk] и построим множество Ξ = {ξ1,...,ξn}. Совокупность (X,Ξ) называют интегральным разбиением отрезка [a,b].
Пусть y = y(x) — заданная на отрезке [a, b ] функция, (X, Ξ) — интегральное разбиение [a, b ] с диаметром δ. Интегральной суммой на интегральном разбиении (X,Ξ) называется число
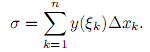
Функция y = y(x) называется интегрируемой по Риману (кратко—интегрируемой) на [a,b], если существует конечный предел I интегральной суммы σ при стремлении диаметра разбиения δ к 0. При этом сам предел I называют определенным интегралом Римана (кратко — интегралом) от y по [a,b] и обозначают
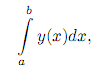
Отрезок [a, b] называют промежутком интегрирования, a и b — соответственно нижним и верхним пределами интегрирования, y(x)dx—подынтегральным выражением.
Теорема 3.1 (Необходимое условие интегрируемости). Если функция y интегрируема на [a,b], то она ограничена на этом отрезке.
Теорема 3.3 (Об интегрируемости непрерывной функции). Всякая непрерывная на отрезке функция интегрируема на этом отрезке.
Геометрический смысл
Пусть y = y(x) — определенная на [a,b] непрерывная неотрицательная функция. Фигуру на плоскости Oxy, ограниченную сверху графиком y = y(x), снизу осью Ox, сбоку прямыми x = a и x = b, называют криволинейной трапецией.
Пусть X — разбиение отрезка [a,b] . На каждой части разбиения [xk−1, xk ] выбираем точку максимума и точку минимума функции y. Интегральные суммы на интегральных разбиениях дают площади многоугольников, состоящих из прямоугольников со сторонами, параллельными осям координат. Первый из этих многоугольников описан около криволинейной трапеции, второй — вписан в трапецию. По теореме об интегрируемости непрерывной функции их интегральные суммы при δ → 0 имеют общий предел
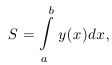который
называют площадью рассматриваемой
криволинейной трапеции.