3. Производные высших порядков. Дифференциал. Дифференциалы высших порядков.

Последовательное дифференцирование

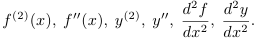Для функции y = f(x) производной второго порядка называют производную функции Обозначают Таким образом,

Для функции y = f(x) производной порядка n называют производную производной порядка n−1. Таким образом

Теорема 2.36 (Формула Лейбница). Если функции u = u(x), v = v(x) имеют производные порядка n, то

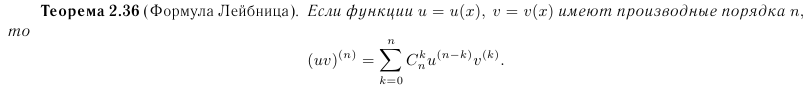
Дифференцирование функций, задаваемых параметрически

Теорема 2.37. Пусть формулы x = ϕ(t), y = ψ(t), t ∈ T задают параметрически функцию y = y(x). Если

функции ϕ(t) и ψ(t) дифференцируемы и ϕ’(t) =/ 0, то функция y = y(x) дифференцируема и ее производная y’(x) задается параметрически формулами

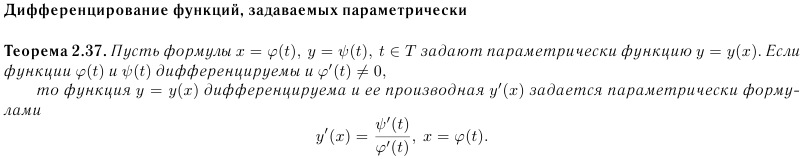
Дифференциалы

Дифференцируемость функции означает, что ее приращение представимо в виде ∆y = A · ∆x + o(∆x).

Главную часть приращения функции называют дифференциалом и обозначают Таким образом,

Дифференциалы старших порядков

Дифференциалы старших порядков. Дифференциалы старших порядков определяются так же, как производные старших порядков.

Вторым дифференциалом функции называют дифференциал от дифференциала. Обозначают d²f(x) или d²y. Таким образом, d²y = d(dy). Второй дифференциал называют также дифференциалом второго порядка.

Дифференциалом порядка n функции называют дифференциал от дифференциала порядка n − 1. Обозначают dnf(x) или dny. Таким образом, dny = d(dn−1y). Дифференциалом нулевого порядка считают d0y = y.

4. Формула Тейлора и ее остаточный член.

Многочлен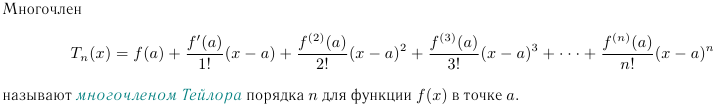

Коэффициенты

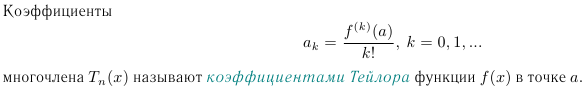многочлена Tn(x) называют коэффициентами Тейлора функции f(x) в точке a.

Теорема 2.39. Если Tn(x) многочлен Тейлора порядка n в точке a, построенный для функции f(x), то

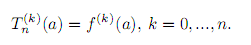
Формула Тейлора Пусть функция f(x) имеет в точке a все производные до порядка n включительно.

Представление функции f(x) в виде

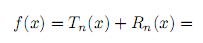
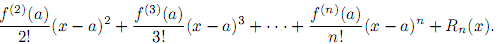
называют формулой Тейлора порядка n в точке a.

Остаточным членом формулы Тейлора называют разность , где Tn(x)многочлен Тейлора.

5. Исследование функций одной переменной. Монотонность, точки экстремума.

Функцию f(x) называют возрастающей на (a,b), если

Функцию f(x) называют строго возрастающей на (a,b), если

Функцию f(x) называют убывающей на (a,b), если

Функцию f(x) называют строго убывающей на (a,b), если

Возрастающую, строго возрастающую функцию, убывающую и строго убывающую функции называют монотонными.

Строго возрастающую функцию, и строго убывающую функции называют строго монотонными.

Критерии монотонности. Пусть f(x) дифференцируемая функция.

Теорема 2.44 (Критерий постоянства). Функция f(x) является постоянной на (a,b) тогда и только тогда, когда f’’(x) = 0, ∀x ∈ (a, b).

Теорема 2.45 (Критерий монотонности). Функция f(x) является возрастающей на (a,b) тогда и только тогда, когда f’(x) >=0, ∀x ∈ (a,b).

Функция f(x) является убывающей на (a,b) тогда и только тогда, когда f’’(x)<=0, ∀x ∈ (a,b).

Теорема 2.46 (Критерий строгой монотонности). Функция f(x) является строго возрастающей на (a,b) тогда и только тогда, когда

2. f'(x) не обращается тождественно в ноль ни на одном интервале из (a,b).

Функция f(x) является строго убывающей на (a,b) тогда и только тогда, когда

2. f'’(x) не обращается тождественно в ноль ни на одном интервале из (a,b)

Если в точке х0 ф-ция определена и при переходе через х0 может менять знак, то точка х0-точка локального экстермума.

+ на – локального максимума

- на + локального минимума

Теорема 2.48 (Первое правило исследования стационарных точек).

Пусть функция f(x) дифференцируема на интервале (a,b) и имеет единственную стационарную точку c ∈ (a, b).

Если f’(x) не меняет знак на (a,b), то f(x) не имеет локального экстремума в точке x0.

Если f’(x) < 0 для a < x < c и f'(x) > 0 для c < x < b, то f(x) имеет в точке c локальный минимум.

Если f’(x) > 0 для a < x < c и f'(x) < 0 для c < x < b, то f(x) имеет в точке c локальный максимум.

Теорема 2.49 (Второе правило исследования стационарных точек).

Пусть функция f(x) имеет на (a,b) вторую производную f’ ’ (x), непрерывную в стационарной

точке c ∈ (a, b).

Если f’ ’ (c) > 0, то f(x) имеет в точке c локальный минимум.

Если f’’ ’ (c) < 0, то f(x) имеет в точке c локальный максимум.

Теорема 2.50 (Третье правило исследования стационарных точек).

Пусть функция f(x) имеет на (a,b) производную f(n)(x), непрерывную в точке c ∈ (a,b), и

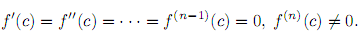
Если число n нечетное, то в точке c экстремума нет.

Если число n четное, то в точке c экстремума есть, причем, если f⁽ⁿ⁾(c) > 0, то в точке c локальный минимум, а если f(n)(c) < 0, то локальный максимум.