
- •1. Дифференцируемость функции в точке. Правила дифференцирования. Таблица производных.
- •2. Основные теоремы о дифференцируемых функциях. Правило Лопиталя.
- •3. Производные высших порядков. Дифференциал. Дифференциалы высших порядков.
- •4. Формула Тейлора и ее остаточный член.
- •5. Исследование функций одной переменной. Монотонность, точки экстремума.
- •6. Исследование функций одной переменной. Направление выпуклости, точки перегиба, асимптоты.
- •7. Первообразная и неопределенный интеграл. Таблица неопределенных интегралов.
- •8. Замена переменных в неопределенном интеграле. Интегрирования по частям.
- •9. Интегральные суммы и определенный интеграл. Условия интегрируемости функций. Геометрический смысл определенного интеграла.
- •10. Классы интегрируемых функций. Свойства определенного интеграла.
- •11. Интеграл с переменным верхним пределом.
- •12. Замена переменных в опред.Интеграле. Интегрирование по частям
- •13. Опреднление вещественного линейного пространства. Примеры
- •14. Линейная зависимость и независимость векторов
- •15. Базис и размерность линейных пространств. Базис n-мерных векторных пространств.
- •16. Базис n-мерных векторных пространств. Координаты вектора
- •17. Преобразования координат
- •18. Линейные отображения и линейные операторы. Примеры линейных отображений и линейных операторов
- •19. Матрица линейного оператора
- •20. Действия над линейными операторами.
- •21. Преобразование матрицы линейного оператора при переходе к новому базису.
- •22. Собственные векторы и собственные значения линейного оператора. Характеристическая матрица и характеристический многочлен.
- •23. Векторное пространство . Расстояние в . Топологические понятия. Последовательности в .
- •24. Понятие функции n переменных. Предел функции n переменных.
- •25. Непрерывность функции n переменных. Основные определения и теоремы.
- •26. Дифференцируемость функции n переменных. Частные производные. Производная по направлению. Градиент.
- •27. Безусловный и условный экстремумы функций двух переменных.
- •28. Площадь фигуры и объем тела.
- •29. Определение двойного интеграла по прямоугольной и произвольной областях.
- •30. Свойства двойного интеграла.
- •31. Сведение двойного интеграла к повторному
- •32. Преобразование фигуры и замена переменной в двойном интеграле. Использование полярных координат.
- •33. Тройной интеграл: определение и свойства. Сведение тройного интеграла к повторному.
- •34. Криволинейный интеграл первого рода. Определение, вычисление и свойства.
- •1. Линейность.
- •35. Определение криволинейного интеграла второго рода и его вычисление
- •36. Свойства криволинейного интеграла второго и его вычисление.
- •37. Формула Грина. Условие Эйлера.
- •38. Числовые ряды. Положительные ряды. Гармонический и геометрический ряды.
- •39. Признаки сравнения для положительных рядов. Признаки Даламбера и Коши.
- •40. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.
- •41. Функциональные последовательности и функциональные ряды. Основные определения.
- •42. Степенные ряды. Теорема Абеля. Радиус сходимости. Ряд Тейлора.
37. Формула Грина. Условие Эйлера.
Пусть в области D ⊂ R2 определены функции P(x,y) и Q(x,y), пусть G ⊂ D — замкнутое связное множество, ограниченное кусочно гладкой кривой L. Зададим на L направление. Направление считают положительным, если при обходе L по такому направлению область G остаётся слева.
Теорема
15.1
(Формула
Грина).
Если P и Q имеют непрерывные частные
производные первого порядка, то
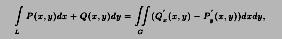
где L обходится в положительном направлении.
Условия Эйлера.
Выражение P(x,y)dx + Q(x,y)dy называют полным дифференциалом в области G, если существует функция, что dF = P(x,y)dx + Q(x,y)dy, ∀(x,y) ∈ G. При этом функцию F называют первообразной для полного дифференциала.
Теорема 15.2. Пусть в односвязной области G заданы функции P(x,y), Q(x,y), имеющие непрерывные производные первого порядка. Тогда следующие четыре условия равносильны:
1) Для любого замкнутого контура L ⊂ G выполняется условие
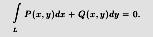
2)
![]() не
зависит от пути интегрирования для
любых A, B ∈
G
не
зависит от пути интегрирования для
любых A, B ∈
G
3) Выражение P(x,y)dx + Q(x,y)dy является полным дифференциалом в области G.
4) Выполнены условия Эйлера: Py'(x, y)=Q'x(x, y), ∀(x,y)∈G.
38. Числовые ряды. Положительные ряды. Гармонический и геометрический ряды.
Числовой ряд.
Пусть задана числовая последовательность (an).
Последовательность сумм S1 = a1, S2 = a1 + a2, S3 = a1 + a2 + a3 и т.д. записывают в виде
![]() и называют числовым рядом с элементами
(или членами) ak.
и называют числовым рядом с элементами
(или членами) ak.
Числовой ряд
называют сходящимся, если существует конечный предел S = limn→∞Sn последовательности частных сумм этого ряда. Если предел не существует или бесконечен, то говорят, что ряд расходится.
Суммой ряда называют предел последовательности его частных сумм.
Условия сходимости ряда.
Если ряд сходится, то limn→∞an = 0
Теорема 20.3. Если сходится ряд, то сходится и любой его остаток.
Положительные ряды
Числовой ряд называют положительным, если все его элементы ak > 0.
Теорема 20.4 (Критерий сходимости положительного ряда). Для сходимости положительного ряда необходимо и достаточно, чтобы последовательность (Sn) его частных сумм была ограничена (сверху).
Гармонический ряд.
Гармоническим
рядом называют ряд ![]() .
Теорема 20.5. Гармонический ряд расходится.
.
Теорема 20.5. Гармонический ряд расходится.
Геометрический ряд.
Если суммировать члены бесконечной геометрической прогрессии 1, q, q2, q3, ..., то получим числовой ряд, который, наряду с гармоническим рядом, служит ориентиром во множестве числовых рядов.
Ряд
![]() q>=0
называют геометрическим рядом. если q
>=1, то ряд расходиться. Если q < 1 - ряд
сходится.
q>=0
называют геометрическим рядом. если q
>=1, то ряд расходиться. Если q < 1 - ряд
сходится.
39. Признаки сравнения для положительных рядов. Признаки Даламбера и Коши.
Первый признак сравнения.
![]() (1)
и
(1)
и ![]() (2)
– положительные ряды
(2)
– положительные ряды
Теорема 20.6.
1. Если сходится ряд 2, то сходится и ряд 1.
2. Если расходится ряд 1, то расходится и ряд 2.
Второй признак сравнения.
Теорема 20.7. Пусть существует предел
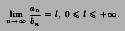
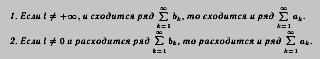
Теорема 20.8. Пусть
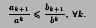
1. Если сходится ряд , то сходится и ряд
2. Если расходится ряд , то то расходится и ряд
Признак Коши.
Положительный ряд .
Теорема 20.9. Пусть существует предел
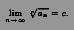
1. Если c < 1, то ряд сходится.
2. Если c > 1, то ряд расходится.
Признак Даламбера.
Положительный ряд .
Теорема 20.10. Пусть существует предел
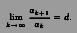
1. Если d < 1, то ряд сходится.
2. Если d > 1, то ряд расходится.
