24. Расчет конических зубчатых передач на выносливость по контактным напряжениям

Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же, как у эквивалент-ного цилиндрического с той же длиной b зуба и профилем, соответствующим среднему дополнительному конусу (среднему сечению зуба). Прочность зубьев определяется зависимостью _H  []_H ,где _H – контактное напряжение; []_H – соот-ветствующее допускаемое напряжение.

Вычисляем расчетное контактное напряжение

,

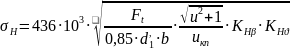где

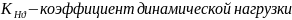
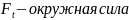
29. Расчет конических зубчатых передач на прочность при изгибе.

32. Шевронные зубчатые передачи. Геометрические параметры, проектирование и расчет. Шевронные колеса

Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Передачи, основанные на таких зубчатых колёсах, обычно называют «шевронными».

Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).

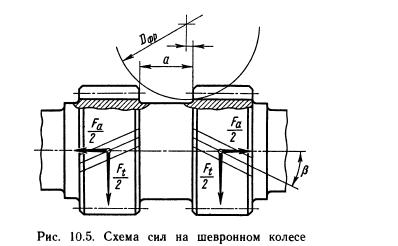
Шевронное колесо представляет собой сдвоенное косозубое колесо, выполненное как одно целое (см. рис. 8.1, в). Вследствие разного направления зубьев на полушевронах осевые силы F_a/2 взаимно уравновешиваются на колесе и на подшипники не передаются (рис. 10.5). Это обстоятельство позволяет принимать у шевронных колес угол наклона зуба β = 25...40°, что повышает прочность зубьев и плавность передачи.

Шевронные зубчатые колеса изготовляют с дорожкой в сере­дине колеса для выхода режущего инструмента (червячной фре­зы на рис. 10.5) или без дорожки (нарезаются долбяком или гребенкой со специальной заточкой, см. рис. 8.1, в).

Шевронные колеса без дорожки нарезают,на специальных малопроизводительных и дорогих станках, поэтому их применяют реже, чем колеса с дорожкой. Ширина дорожки а= (10... 15)/п.

Шевронный зуб требует строго определенного осевого поло­жения шестерни относительно колеса, поэтому вал одного из колес пары монтируют в подшипниках, допускающих осевую «игру» вала.

Недостатком шевронных колес является большая стоимость их изготовления. Применяются в мощных быстроходных закры­тых передачах.

Рис. 10.5. Схема сил на шевронном колесе

Геометрический и прочностной расчеты шевронной передачи аналогичны расчетам косозубой передачи. Для шевронной пе­редачи коэффициент ширины обода колеса ψ_α = 0,4...0,8.

32. Планетарные зубчатые передачи с внутренним и наружным зацеплением зубьев.

Планетарные зубчатые передачи — такие, в которых имеются зубчатые колеса с перемещающимися геометрическими осями. Простейшая планетарная передача (рис. 4.15, а) состоит из вращающегося центрального (солнечного) колеса 1 с наружным зацеплением, неподвижного центрального колеса 3 с внутренним зацеплением и водила Н, на котором закреплены оси сателлитов 2 (3—6 штук). Колеса 1 и 3 называют центральными. Сателлиты совершают планетарное движение, т. е. вращаются вокруг своих осей и вокруг колеса 7. При неподвижном колесе 3 движение может передаваться от колеса 1 к водилу Н и наоборот. При неподвижном водиле получается простая зубчатая передача. Если в планетарной передаче подвижны оба центральных колеса и водило, то такую передачу называют дифференциальной.

Передаточное число планетарных передач удобнее всего определять методом остановки водила. По этому методу всем звеньям передачи условно сообщается дополнительное вращение с угловой скоростью водила, но обратной по знаку. Тогда получают так называемый приведенный механизм с неподвижным водилом, представляющий собой простую зубчатую передачу.

 

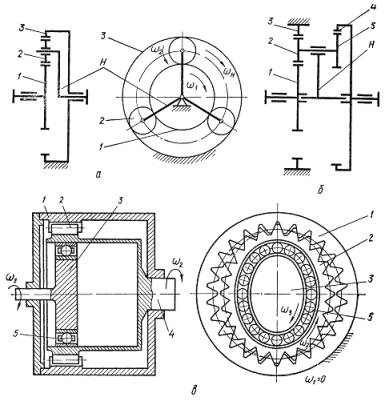
Рис.4.15

При определении передаточного числа принимают знак «плюс», если все звенья передачи вращаются в одну сторону, и знак «минус»,— если в разные стороны.

Передаточное число u' приведенного механизма (рис. 4.15, а)

,

где   ,   -угловые скорости соответственно колес 1 и 3;

- угловая скорость водила;

z₁, z₃-числа зубьев соответственно колес 1 и 3.

В действительной передаче водило вращается, а колесо 3 закреплено,   т. е.  .

Передаточное число и планетарной передачи:

б

где

.

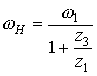Подобным образом определяются передаточные числа и для других видов планетарных передач.

Для двухступенчатой планетарной передачи (рис. 4.18,ж), в которой каждая ступень выполнена по рис. 4.15, а, передаточное число определяется по формуле

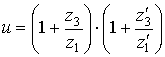б

где   ,  — соответственно числа зубьев колес 1' и 3' (рис. 4.18, ж).

Планетарная передача, выполненная по рис. 4.15, б, состоит из трех центральных колес 1, 3, 4 и сдвоенного сателлита 2 и 5. В этой передаче можно получить значительные передаточные числа [для силовых передач u= 19 — 352 при h=0,85 — 0,95, для кинематических u < 1500 при очень низких к. п. д. (h < 0,1)].

Основными достоинствами планетарных передач являются возможность осуществления значительных передаточных чисел, компактность, небольшая масса и пр.

Однако планетарные передачи требуют повышенной точности изготовления и сложны в сборке. К. п. д. их резко падает с повышением передаточного числа. Планетарные передачи применяют в автомобилях, металлорежущих станках, приборах и т. П.