23. Расчет цилиндрических зубчатых колес на контактную прочность

Вследствие наклона зубьев в зацеплении одновременно находится несколько пар зубьев, что уменьшает нагрузку на один зуб, повышая его прочность (снижая расчётные напряжения). Аналогично расчету прямозубой передачи межосевое расстояние для косозубых колес определяют по формуле (2.3.17):

,

где Ка = 43 МПа – для косозубых колес. Контактные напряжения в поверхностном слое зубьев

,

где   - коэффициент нагрузки при расчете по контактным напряжениям; - 1,04 – 1,13 коэффициент нагрузки, учитывающий распределение нагрузки между зубьями и зависит от окружной скорости;   - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий); для косозубых передач выбирается с учетом расположения колеса на валу и термообработки;  - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки  =1,02-1,06 при любой твердости, скорость до 10 м/с,  =1,1 при твердости поверхности не больше 350 НВ и скорости 10-20 м/с,  =1,05 при твердости более 350 НВ и скорости 10-20 м/с. Косозубые передачи работают более плавно, чем прямозубые, поэтому коэффициент   , меньше.  Условие контактной прочности косозубой передачи 

,

Если условие не выполняется, то изменяют ширину венца колеса b2, не выходя за пределы рекомендуемых значений  . Если это не даст желательного результата, то либо назначает другие материалы колёс или другую термообработку, и расчёт повторяют. Расчет допускаемых напряжений ведется аналогично расчету прямозубых колес

24. Расчет цилиндрических зубчатых колес на изгибную прочность.

Наибольшие напряжения изгиба в одном из сопряженных зубьев возникают в начальный или конечной момент их зацепления. Зуб рассматривается как консольная балка, нагруженная нормальная силой с опасным сечением а-в у основания зуба (рис. 60). Зуб представляет собой короткую широкую консоль, размеры опасного сечения соизмеримы с ее высотой. Для упрощения задачи напряжение изгиба определяется в соответствии с классической теорией изгиба, в основу которого положена гипотеза плоских сечений. Все величины, входящие в расчетную формулу выразим через перпендикулярные составляющие F_r и F_t. Составляющая F_t, направленная перпендикулярно оси симметрии профиля и вызывает поперечный изгиб зуба. Составляющая F_r ~ вдоль оси симметрии и вызывает сжатие зуба (без учета сил трения F_r= F_ttg ). Напряжение сжатия от силы F_r невелико, составляет не более 4...6% от напряжения изгиба. Поэтому напряжение сжатия в расчете не учитывается, что компенсируется введением в расчет составляющей F_t, которую принимают больше фактической. Выразим составляющую F_t через расчетный крутящий момент на шестерне: F  

где l пренебрегаем, т.к. l<<d< b=""></d<>_1/2. Для составления уравнения прочности необходимо знать положение опасного сечения зуба, для определения опасного сечения в профиль зуба вписывается профиль балки равного сопротивления – очерченный квадратной параболой. Эта парабола вписывается таким образом, чтобы ее вершина совпадала с точкой приложения A силы F , а ветви касались профиля зуба. Не заштрихованное параболистическое тело проходит через точки m n касания параболы с профилем зуба (здесь прочность зуба и параболы одинаковая). Обозначив расстояние от опасного сечения m n до точки приложения силы F_t через h и используя классическую теорию изгиба можно записать следующим образом уравнение прочности: M  или F ,   

Для того, чтобы учесть различие законов распределения напряжений в опасном сечении зуба линейного принятого в классической теории изгиба и не линейного фактического – в левую часть уравнения введем теоретический коэффициент концентрации напряжения у основания зуба К_T, значение которого зависит от формы и радиуса переходной кривой, а также коэффициенты: К  - коэффициент концентрации напряжения у основания зуба; - коэффициент перекрытия; K  - коэффициент колебания длины контактной линии; К  - коэффициент концентрации напряжения. Выразим размеры зуба a и h через шаг p: a= , h= , p= Тогда уровнение будет иметь вид: F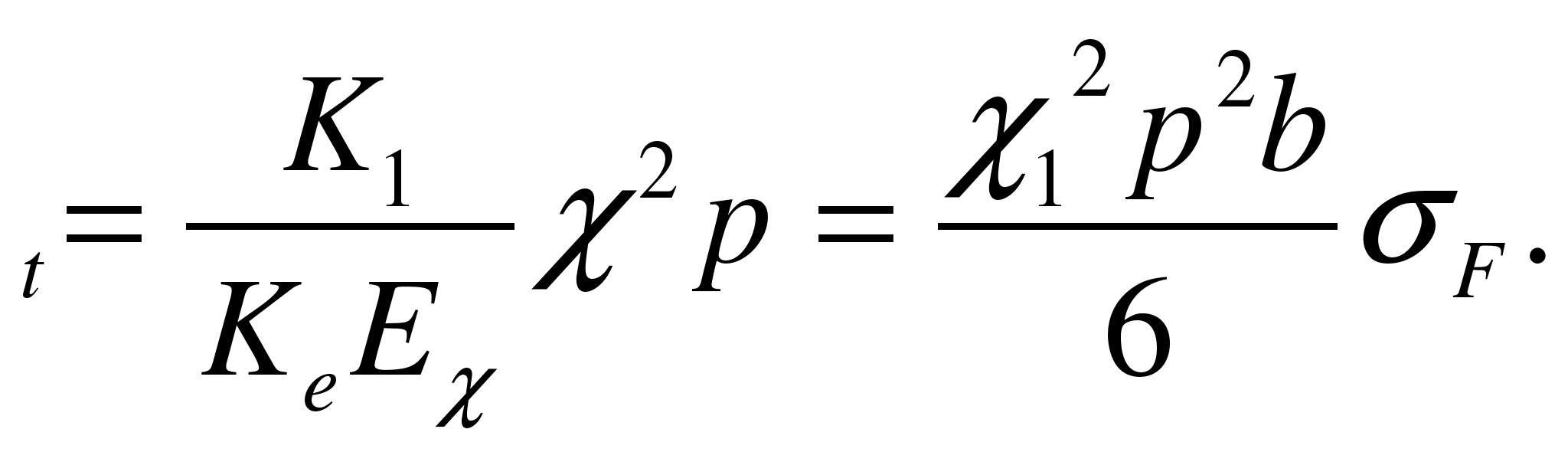     - коэффициент формы зуба; - коэффициент перекрытия зуба; w - удельная окружная сила, Н/мм Тогда получим