10. Допущения метода послойного суммирования. Допущения метода послойного суммирования

Условность метода послойного суммирования определяется большим количеством различных допущений, положенных в его основу, основными из которых являются следующие:

1) вертикальные давления σ_Z в пределах каждого отдельного слоя принимаются равномерно распределенными по горизонтальной плоскости, тогда как в действительности эпюры распределения давлений имеют максимум в центре и уменьшаются к краям фундамента;

2) вертикальные давления σ_Z в пределах каждого слоя принимают равными величине максимального давления по оси действия внешней нагрузки, без учета их затухания в стороны от оси;

3) при вычислении величины осадки учитывается только действие вертикальных напряжений, тогда как в действительности и горизонтальные и касательные напряжения тоже вызывают деформации грунта;

4) осадки учитываются только в пределах условно принятой сжимаемой толщи, без учета деформаций, фактически происходящих и за ее пределами.

Очевидно, что первые два допущения приводят к некоторому завышению расчетной величины осадки, а вторые два к ее снижению. В целом осадки, вычисленные методом послойного суммирования, достаточно хорошо совпадают по величине с фактическими осадками сооружений.

11. Фазы напряженного состояния грунтов Фазы напряженного состояния грунтов.

Как известно грунтовая среда характеризуется нелинейностью диаграммы деформирования. Обычно при расчетах рассматривается линейно деформируемая грунтовая среда основания. Такая линейная постановка задачи может быть использована при незначительных давлениях на основание, при которых преобладают деформации уплотнения основания и осадки увеличиваются по закону близкому к прямой пропорциональности между осадкой и давлением (Рис. 1). Напряженное состояние для этого случая относят к I фазе - уплотнения и локальных сдвигов. На рис.1. первой фазе соответствует участок ОА. При дальнейшем увеличении давления выделяется II фаза – фаза развития значительных сдвигов (участок АВ).

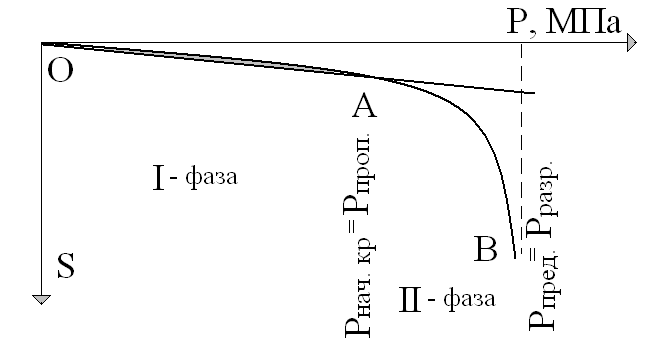
Рис.1. Диаграмма осадок и фазы напряженного состония.

Граница, разделяющая I и II фазы, служит для оценки начального критического давления Р_{нач кр}, до которого преобладают безопасные для прочности грунтового основания деформации уплотнения. В I-й фазе ни в одной точке объема основания не развиваются пластические деформации. Грунты находятся в устойчивом состоянии. И только здесь, в этой фазе, возможно (с определенной потерей точности) использовать линейную зависимость между напряжениями и деформациями (Р_{нач кр} = Р_проп) и теорию линейно деформируемых тел.

Во II-й фазе деформации уплотнения сопровождаются значительным развитием деформаций сдвига, которые вызывают местные потери устойчивости по объему основания. При дальнейшем увеличении давления грунт переходит в состояние предельного равновесия, которое соответствует предельному давлению на основание Р_пред. При действии предельного давления происходит полное использование несущей способности основания (точка В на рис.1). На участке АВ наблюдается настолько нелинейное деформирование, что использовать линейные зависимости не представляется возможным.

12. Уравнения предельного равновесия.

Уравнения предельного равновесия.

При определенном сочетании напряжений в грунте может возникнуть предельное равновесное напряженное состояние. Предельное напряженное состояние такое, при котором малейшее добавочное силовое воздействие или малейшее изменение прочности грунта приводит к нарушению существующего равновесия и потере устойчивости массива грунта.

В качестве основного условия предельного состояния принимают условие, сформулированное в 1773 г. Ш. Кулоном, связанное с возможностью начала скольжения одних масс грунта относительно других по площадкам, на которых действуют касательные и нормальные напряжения, связанные зависимостью (Рис. 2)

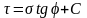(1)

где 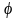и С – параметры линейной зависимости, условно называемые углом внутреннего трения и сцеплением. Для несвязных грунтов С = 0.

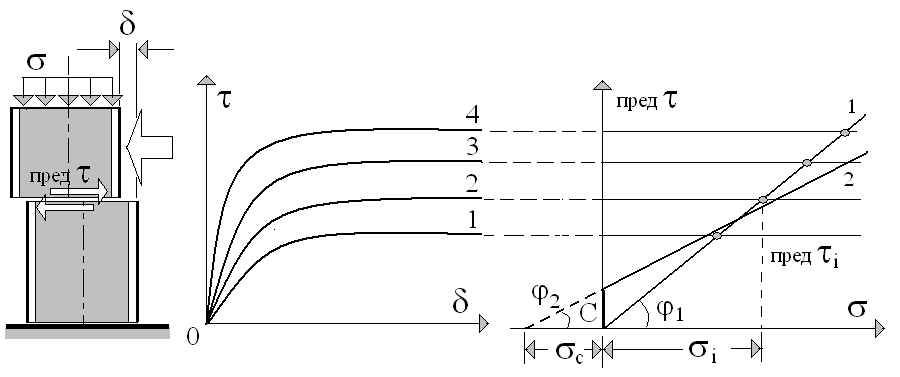
Рис. 2. Сопротивление сыпучих и связных глинистых

грунтов сдвигу

В некоторых случаях удобно представлять условие предельного равновесия в форме

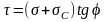(2)

где 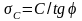- напряжение всестороннего сжатия, эквивалентное связанности (фиктивная величина).

Зависимость Кулона для грунтов (1) является частным случаем появившейся позднее теории прочности Мора, где сопротивление сдвигу по какой-либо площадке является функцией нормального напряжения

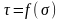(3)