7. Одномерная задача теории компрессионного уплотнения. Одномерная задача теории компрессионного уплотнения

Сжатие слоя грунта рассматривается в условиях невозможности бокового расширения при действии с поверхности безграничной по площади равномерно распределенной нагрузки. Ограниченной мощности слой сжимаемого грунта подстилается снизу скалистым основанием (Рис. 1). В этом случае сжатие грунта слоя будет аналогично сжатию в условиях компрессионных испытаний.

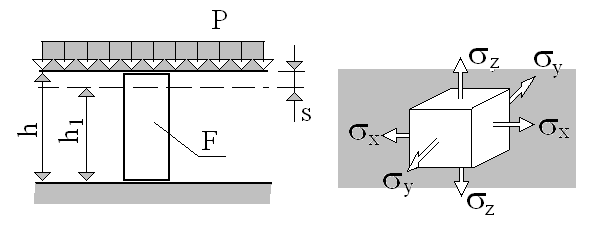
Рис. 1. Схема сжатия слоя грунта при сплошной нагрузке в условиях сжатия без возможности бокового расширения

Из рисунка видно, что полная величина осадки

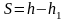(1)

где h – мощность сжимаемого слоя до обжатия его внешним давлением, h₁ – мощность сжимаемого слоя после обжатия.

Объем скелета грунта в единице объема грунта

Объем скелета в выделенной грунтовой массе в виде призмы площадью F до и после деформации остается постоянным

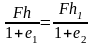
Из этого условия можно найти h₁

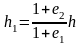(2)

где F – площадь грунтовой призмы;

е₁ – коэффициент пористости грунта до приложения нагрузки;

е₂ – коэффициент пористости грунта после окончания осадки под нагрузкой

Подставляя (2) в (1) получаем

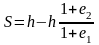
Или

Из результатов компрессионных испытаний можно положить, что

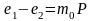
где m₀ – коэффициент уплотнения (сжимаемости).

Тогда формула для величины конечной осадки примет вид

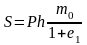
Или

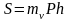(3)

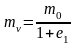где - коэффициент относительной сжимаемости, зависящий только от компрессионных свойств грунта.

Таким образом, для вычисления величины осадки используются результаты компрессионных испытаний для оценки сжимаемости грунта и коэффициента уплотнения.

Величину осадки можно также найти по результатам полевых испытаний в которых определяется модуль общей деформации грунта Е₀.

При принятой схеме сжатия слоя грунта (Рис. 1)

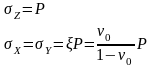(4)

где - коэффициент бокового давления;

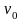- коэффициент бокового расширения.

Из курса сопротивления материалов следует, что относительная деформация грунта 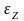вдоль оси Z, совпадающей с направлением действия силы Р,

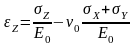(5)

Подставив (4) в (5), получим

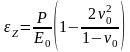
Или, вводя обозначение

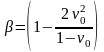
Получим

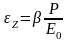
Полная величина осадки равна произведению относительной осадки на мощность деформируемого слоя

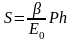(6)

здесь 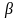- коэффициент, зависящий только от свойств грунта и вычисляемый на основе опытного определения коэффициента бокового давления или коэффициента бокового расширения .

Сравнивая (3) и (6) можно найти зависимость между 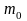и Е₀:

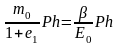
Отсюда следует

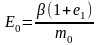
Данная зависимость устанавливает обратную пропорциональность величин Е₀ .

8. Метод эквивалентного слоя. Метод эквивалентного слоя

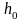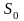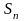Эквивалентным слоем грунта называется слой, осадка которого при сплошной нагрузке равна осадке фундамента на мощном массиве при местной нагрузке на полупространстве:

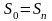(7)

При сплошной нагрузке относительная деформация слоя грунта

Отсюда следует

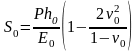. (8)

С другой стороны, осадка реального фундамента на мощном массиве грунта или слое грунта ограниченной мощности

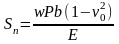, (9)

где w – коэффициент формы и жесткости;

b − ширина загруженной площади.

Подставляя в выражение (7) значения (8) и (9) и решая уравнения относительно h₀, получим

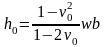. (10)

вводя обозначение

,

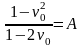Получим формулу для определения мощности эквивалентного слоя грунта

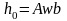, (11)

где b − ширина фундамента.

Из формулы (11) видно, что мощность эквивалентного слоя грунта зависит от бокового расширения грунта (коэффициент А), от формы и жесткости фундамента (коэффициент w) и пропорциональна ширине фундамента.

С учетом (11) получим формулу для определения осадки фундамента заданных размеров

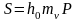. (12)

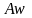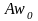Значения коэффициента эквивалентного слоя табулированы для определения максимальных и средних осадок гибких фундаментов ( , ) и осадок абсолютно жестких фундаментов (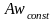 ) в зависимости от отношения сторон фундамента l/b и коэффициента Пуассона v₀ . Следует отметить, что существуют следующие соотношения между коэффициентами:

для круглых и квадратных фундаментов

;

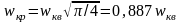между коэффициентами эквивалентного слоя для центра прямоугольной площади абсолютно гибкой нагрузки и ее угловой точки существует простое соотношение

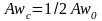, (13)

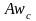где − коэффициент эквивалентного слоя для угловой точки.