Задача о действии одной сосредоточенной силы (задача Буссинеско) Задача о действии одной сосредоточенной силы (задача ж. Буссинеско)
Рассматривается действие сосредоточенной силы Р, приложенной перпендикулярно к ограничивающей полупространство плоскости. Полупространство однородно в глубину, в стороны и обладает линейной деформируемостью (рис. 1).
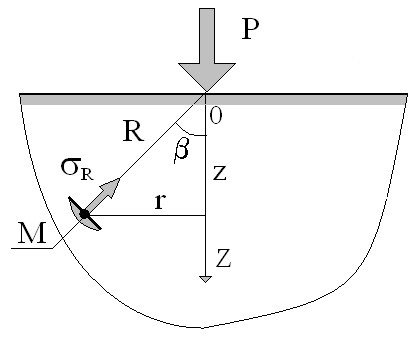
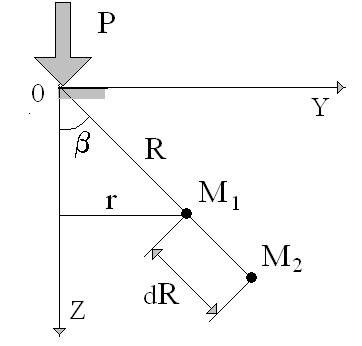
Рис. 1. Расчетная схема действия сосредоточенной силы
Для любой точки полупространства с координатами Z, Y или , R (например М1 и М2) перемещения точек по направлению радиуса R равно:
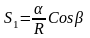
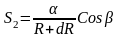(1)
Относительная деформация грунта на отрезке dR :
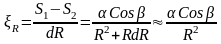(2)
Для линейно деформируемой среды напряжение пропорционально деформации
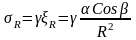(3)
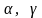- коэффициенты
пропорциональности.
Напряжения в массиве грунта связаны с величиной силы Р условиями равновесия. Для составления уравнения равновесия проведем полушаровое сечение с центром в точке приложения сосредоточенной силы (рис. 2).
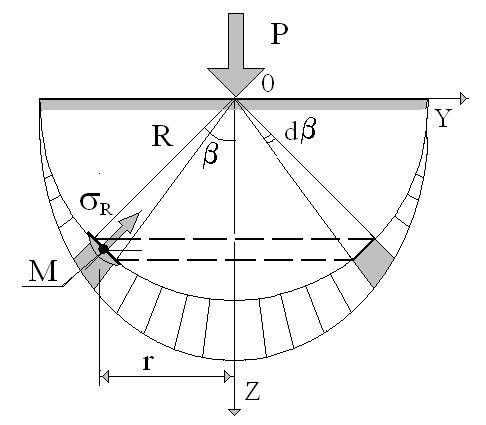
Рис. 2. Схема радиальных напряжений при действии сосредоточенной силы.
Для выделенного элементарного шарового пояса с центральным углом d радиальное напряжение принимается постоянным.
Условие равновесия – сумма проекций всех сил на вертикальную ось равна нулю:
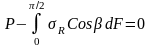(4)
dF – площадь кольца полушария при увеличении угла на величину d:
(5)
Тогда:
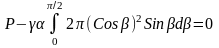(6)
После вычисления интеграла получим:
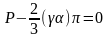(7)
Отсюда следует, что
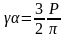(8)
Поставляя найденные коэффициенты пропорциональности в (3) получим выражение для радиального напряжения
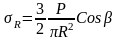(9)
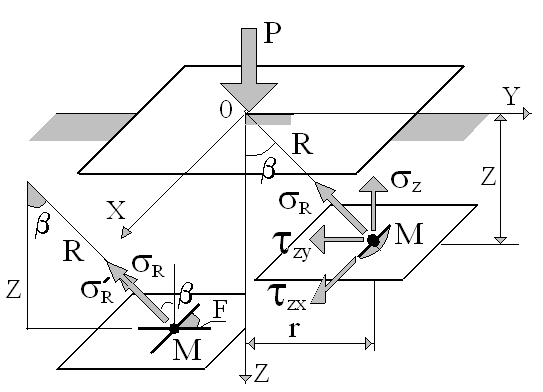
Рис. 3. Составляющие напряжений для площадки, параллельной ограничивающей плоскости.
Радиальное
напряжение, отнесенное к площадке
параллельной ограничивающей плоскости,
обозначим
.
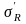Из геометрических соотношений
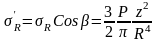(10)
Разложим
силу
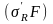на три направления z,
x,
y:
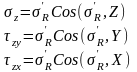(11)
Учитывая, что
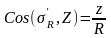
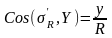
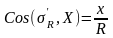(12)
получим величины составляющих напряжений для площадки, параллельной ограничивающей плоскости:
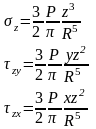(13)
Вывод:
компоненты напряжений
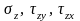для площадок, параллельных ограничивающей
полупространство плоскости, не зависят
от упругих постоянных однородного
линейно деформируемого полупространства.
Принимая во внимание, что
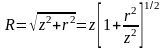(14)
и обозначив
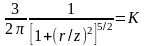(15)
получим,
широко используемое на практике при
расчете осадок фундаментов простое
выражение для сжимающих напряжений
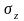
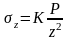(16)
Для облегчения расчетов значения коэффициента К сведены в таблицу [].
Рассмотрим действие сосредоточенной силы Q, приложенной на поверхности параллельно ограничивающей полупространство плоскости (рис.4.)
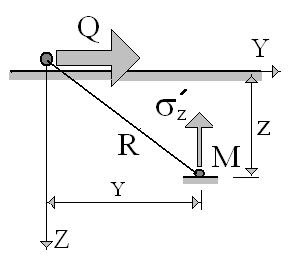
Рис. 4. Схема действия сосредоточенной силы Q.
Сжимающие напряжения при действии горизонтальной силы
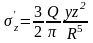(17)
Имея выражения для сжимающих напряжений при действии вертикальной и горизонтальной сил можно найти сжимающие напряжения ля наклонной силы.