Московский авиационный институт

(национальный исследовательский университет)

филиал «Стрела»

Курсовая работа по вычислительной математике Решение краевой задачи для обыкновенного дифференциального уравнения

Вариант № 10

Выполнил студент группы С-201С Черников Д.В.

Принял преподаватель Наливайко А. Г.

2013 Г. Г. Жуковский Содержание:

1.Постановка задачи……………………………………………………………………………..3

2.Метод сведения краевой задачи к задаче Коши:

2.1. Описание метода…………………………………………………………………….5

2.2. Описание результатов……………………………………………………………….9

3.Метод конечных разностей:

3.1. Описание метода…………………………………………………………………….

3.2. Описание результатов……………………………………………………………….

4.Выводы..………………..…………………………………………………………………...16

Приложение 1. Листинг программы «Метод сведения краевой задачи к задаче Коши»

Приложение 2. Листинг программы «Метод конечных разностей»

1. Постановка задачи

Дано линейное дифференциальное уравнение второго порядка:

(1.1)

с краевыми условиями:

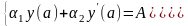(1.2)

где функции P(x), Q(x), F(x) непрерывны, и 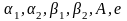- заданные постоянные, причем: 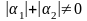и .

Требуется найти решение y(x) уравнения (1.1), удовлетворяющее краевым условиям (1.2).

В данном варианте курсовой работы необходимо:

Решить краевую задачу для обыкновенного дифференциального уравнения с точностью Е=1.е-4. Проверить достигнутую точность. Результаты представить с шагом h=0.02. Решение провести тремя следующими методами:

Сведением краевой задачи к задаче Коши.

Методом конечных разностей.

y''+3,8xy'-0,6y/x²=-1,9; y(1,4)=-3; y(1,8)=2 (1.3)

Из условий следует, что функции P(x) = 3,8*x; Q(x) = -0,6/x*x ; F(x) = -1,9 и постоянные

1 = 1, 2 = 0, 1 = 1, 2 = 0, a =1,4, b =1,8, A = -3, B = 2.

2. Метод сведения краевой задачи к задаче Коши

2.1. Описание метода

Согласно данному методу краевая задача сводится к задаче Коши, решение которой осуществляется методом Рунге-Кутта. Суть метода в том, что первое решение при последовательном изменении аргумента и повторении вычислений становится точнее. А метод Рунге-Кутта метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок   .

Чтобы свести краевую задачу (1.1)-(1.2) к задачам Коши решение дифференциального уравнения (1.1) с краевыми условиями (1.2) будем искать в виде линейной комбинации:

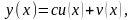где c=const (2.1)

Подставим y(x) в виде (2.1) в исходное дифференциальное уравнение (1.1) и сгруппируем слагаемые при постоянной с, получим выражение:

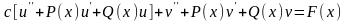(2.2)

Потребуем, чтобы равенство (2.2) выполнялось при любом с, для этого необходимо, чтобы коэффициенты при постоянной с обращались в ноль, получим систему уравнений:

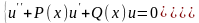(2.3)

Чтобы свести краевую задачу (1.1)-(1.2) к задачам Коши для функций u=u(x) и v=v(x), подставим в первое краевое условие (1.2) выражение для функции y(x) и сгруппируем слагаемые при постоянной c, будем иметь:

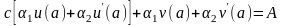(2.4)

Для того чтобы равенство (2.4) было справедливо при любом с, необходимо и достаточно, чтобы коэффициенты при постоянной с обращались в ноль, т. е. должны быть выполнены равенства:

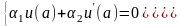(2.5)

Получили систему (2.5) из двух уравнений с четыремя неизвестными. Решений системы будет бесконечное множество. Найдем хотя бы одно.

Для обеспечения первого равенства системы, например, можно подобрать:

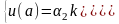(2.6)

где постоянная k отлична от нуля.

Для выполнения второго равенства системы (2.5) положим

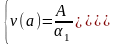
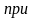
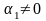(2.7)

или

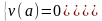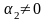при (2.8)

По условию курсовой работы 1 = 1, 2 = 0, A = -3 при k = -1 будем иметь:

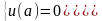(2.9)

v(a)=-3;

v'(a)=0 (2.10)

Отсюда видно, что u должно быть решением задачи Коши (2.9) для однородного уравнения (2.3), удовлетворяющее начальным условиям (2.6), а v должно быть решением задачи Коши (2.10) для неоднородного уравнения (2.3), удовлетворяющее начальным условиям (2.7) или (2.8). При этом для любого с функция y=cu+v удовлетворяет краевому условию на конце x=a.

Подберем теперь постоянную c так, чтобы функция y(x) удовлетворяла краевому условию (1.2) на конце отрезка (a;b) при x=b.

,

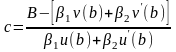при этом предполагается, что знаменатель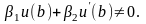

Так как по условию работы ₁ = 1, 2 = 0, то коэффициент c будет иметь вид:

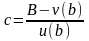
Для решения полученных уравнений из системы (2.3) будем использовать метод Рунге-Кутта, который имеет достаточно высокую точность на всем интервале порядка

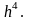
Рассмотрим второе дифференциальное уравнение из системы (2.3) с начальным условием (2.7). Дифференциальные уравнения системы (2.3) являются однотипными, поэтому решение первого уравнения системы (2.3) с начальным условием (2.6) осуществляется аналогичным способом, при условии .

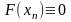Для того чтобы решить указанное дифференциальное уравнение методом Рунге-Кутта, сделаем замену:

и подставим ее во второе дифференциальное уравнение из системы (2.3), получим:

,

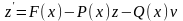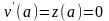
Расчет производим следующим образом: выберем шаг h, приращение x в зависимости от шага будет:

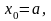
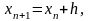где n=0,1…k-1

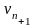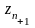Соответствующие значения и искомых функций v и z определяются формулами:

где:

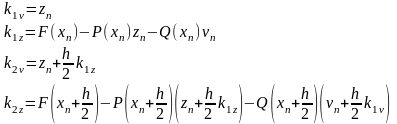
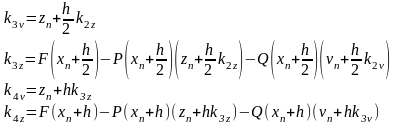
Чтобы достичь заданную точность вычисляем y(x): один раз с шагом h, другой раз с шагом h/2, получая при этом более точные значения. Если max расхождение полученных значений не превышает заданной точности Е =1.e-4, то выбранный шаг h можно считать достаточным и полученная функция y(x) удовлетворяет заданной точности. Иначе уменьшаем шаг h, пока не будет достигнута заданная точность.