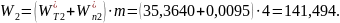- •Содержание
- •1.2. Частота вращения вала двигателя
- •Введение
- •1. Выбор электродвигателя и расчет основных параметров привода
- •1.1. Выбор электродвигателя
- •2.2. Расчет допускаемых напряжений
- •2.3. Проектный расчет передачи
- •2.4. Проверочный расчет передачи
- •2.5. Расчет длины общей нормали
- •3. Расчет клиноременной передачи
- •4. Расчет и проектирование валов
- •4.1. Проектный расчет валов
- •4.2. Эскизная компоновка
- •4.3. Построение эпюр изгибающих и крутящих моментов
- •4.4. Уточненный расчет валов
- •5. Расчет подшипников на долговечность
- •6. Проверка прочности шпоночных соединений
- •7. Расчет элементов корпуса редуктора
- •8. Смазка зубчатой передачи и подшипников
- •9. Уплотнительные устройства
- •10. Сборка редуктора
- •Библиографический список
2.3. Проектный расчет передачи
Межосевое расстояние передачи определяем из расчета на выносливость по контактным напряжениям:
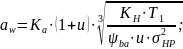
где Т1 – крутящий момент на шестерне, Т1 = 166,4Н·м;
Кн – коэффициент контактной нагрузки, Кн = 1,2;
Ψba – коэффициент ширины зубчатого венца, Ψba = 0,4 из ряда по
ГОСТ 2185-66;
u – передаточное число, u = 1,55;
σНР – допускаемые контактные напряжения, σНР = 515,5 МПа.
Тогда:
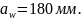
Модуль, числа зубьев колес и коэффициенты смещения
Рекомендуемый диапазон для выбора модуля:
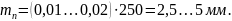
Из
полученного диапазона выберем стандартный
модуль
 =2
=2
([1], табл. 5.1, с.11).
Суммарное число зубьев передачи:
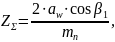
 = 15о для
прямозубых передач.
= 15о для
прямозубых передач.

Определим делительный угол наклона зуба:
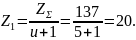
Число
зубьев колеса
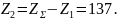
Фактическое передаточное число:
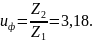
При u > 4,5 отличие фактического передаточного числа от номинального должно быть не больше 4%.
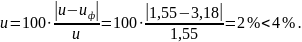
Поскольку
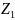 >
17, примем коэффициенты смещения x1
= 0 и x2
= 0.
>
17, примем коэффициенты смещения x1
= 0 и x2
= 0.
Ширина зубчатых венцов и диаметры колес
Ширина зубчатого венца:
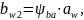
где
 – коэффициент ширины зубчатого венца,
=
0,4;
– коэффициент ширины зубчатого венца,
=
0,4;
 – межосевое расстояние,
= 180 мм.
– межосевое расстояние,
= 180 мм.
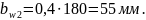
Примем
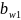 = 66 мм.
= 66 мм.
Определим диаметры окружностей зубчатых колес.
Диаметры делительных окружностей для косозубых колес:


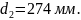
 Диаметры
окружностей вершин и впадин зубьев
колес внешнего зацепления:
Диаметры
окружностей вершин и впадин зубьев
колес внешнего зацепления:
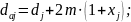
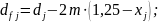
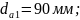
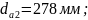

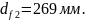
Окружная скорость в зацеплении и степень точности передачи:
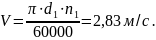 Для
полученной окружной скорости назначим
степень точности передачи
Для
полученной окружной скорости назначим
степень точности передачи
nст = 8 ([1], табл. 8.1, с.14), учитывая, что для закрытых зубчатых передач nст = 9 применять не рекомендуется.
2.4. Проверочный расчет передачи
Проверка изгибной прочности зубьев
Напряжения изгиба в зубе шестерни:

где
 – коэффициенты формы зуба;
– коэффициенты формы зуба;
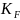 – коэффициент формы зуба;
– коэффициент формы зуба;
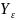 – коэффициент, учитывающий перекрытие
зубьев;
– коэффициент, учитывающий перекрытие
зубьев;
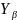 – коэффициент, учитывающий влияние
угла наклона зуба на его
– коэффициент, учитывающий влияние
угла наклона зуба на его
прочность.
Коэффициент
формы зуба при

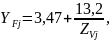
где:


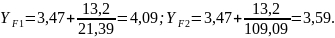
Коэффициент, учитывающий влияние угла наклона зуба на его прочность:

Коэффициент торцевого перекрытия:

 Коэффициент,
учитывающий перекрытие зубьев:
Коэффициент,
учитывающий перекрытие зубьев:
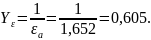
Коэффициент нагрузки при изгибе:
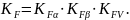
Для определения составляющих коэффициента используем следующие зависимости:


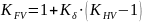 при НВ2
< 350.
при НВ2
< 350.
Для
косозубых передач
 = 3.
= 3.
В результате получим:
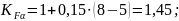
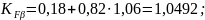
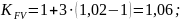
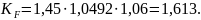
Тогда:

условие изгибной прочности выполняется.
Напряжения изгиба в зубьях колес:
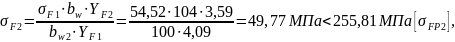
условие изгибной прочности выполняется.
Силы в зацеплении
Окружная сила:
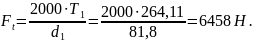
Распорная сила в косозубых передачах:
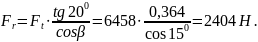
Осевая сила в косозубых передачах:

2.5. Расчет длины общей нормали
Постоянная хорда:
|
([5], с.407) |
где
 угол зацепления,
угол зацепления,

 модуль зацепления,
модуль зацепления,
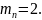
 Тогда:
Тогда:

Высота до постоянной хорды:
 ([5], табл. 12)
([5], табл. 12)
Условное
число зубьев

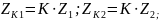
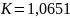 ([5], табл. 13).
([5], табл. 13).
Тогда:
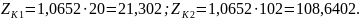
Часть
длины общей нормали, определяемая целой
частью
 величины
величины
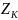 ,
выраженная в долях модуля:
,
выраженная в долях модуля:
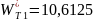 ([5], табл. 14) при
([5], табл. 14) при
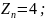
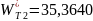 ([5], табл. 14) при
([5], табл. 14) при
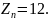
Часть длины общей нормали, определяемая дробной частью величины , выраженная в долях модуля:
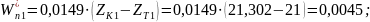

Длина общей нормали: