Тема 2. Определение напряжений в грунтах от внешних сил.

Нахождение напряжений в грунтах от внешних сил связано с решением непростой проблемы расчета осадок оснований. Передаваемые на грунты нагрузки в общем случае произвольно распределяются по площадкам, имеющим разную форму и различные с размеры. Любое давление представляет сложное загружение, которое, каким бы оно не было, можно привести к более простому виду. Элементарным видом нагрузки, служащим основой для таких преобразований, является сосредоточенная сила. Сущность приема заключается в том, что давление на всей площади, или, если её разделить, то на отдельных участках, заменяется одной или несколькими, по числу участков, равнодействующими силами. Возможностей перехода от распределенного давления к загружению сосредоточенными силами неограниченно. Следует уяснить, что во всех случаях свойства грунтов идеализируются:

• грунтовый массив считается однородным, сплошным, изотропным, материалом;

• при загружении грунтовый массив деформируется линейно.

Методы определения напряжений можно применять при нагрузках или давлениях, при которых различия между идеализированным и природным грунтом не существенны.

Предметом самостоятельно изучения являются методы определения вертикальных напряжений σ_z, которые используются в расчетах осадки, от следующих видов нагрузок:

• от сосредоточенной силы;

• от группы сосредоточенных сил (метод элементарного суммирования);

• от равномерно распределенной нагрузки по прямоугольной площадке с различным соотношением сторон.

2.1. Напряжения от сосредоточенной силы на поверхности грунта (рис. 2.1).

На основе принятых допущений напряжения в любой произвольно взятой точке М вычисляются по следующей формуле:

σ_z = kР, (2.1)

где k – коэффициент, подсчитываемый по формуле

k = , (2.2)

или принимается по таблице (10) в зависимости от отношения r / z.

Таблица 2.1

Значения коэффициента. k

r / z	k	r / z	k	r / z	k
0.00	0.4775	0.36	0.3521	0.72	0.1681
0.04	0.4756	0.40	0.3294	0.76	0.1527
0.08	0.4699	0.44	0..3068	0.80	0.1386
0.12	0.4607	0.48	0.2843	0.84	0.1257
0.16	0.4482	0.52	0.2625	0.88	0.1138
0.20	0.4329	0.56	0.2414	0.92	0.1031
0.24	0.4151	0.60	0.2214	0.96	0.093
0.28	0.3954	0.64	0.2024	1.00	0.0844
0.32	0.3742	0.68	0.1846	1.04	0.0764

Рис. 2.1. .Расчетная схема для определения σ_z

Примечание: значения k для более широкого диапазона изменения r/z приведены в Справочнике проектировщика «Основания и фундаменты». М. – 1964 г. (табл. 5.1 стр. 85)

От нескольких сил напряжения в некоторой точке М определяются в соответствии со схемой на рис 2.2.

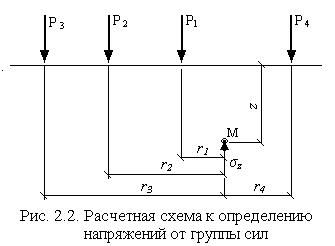
Величина напряжения вычисляется как сумма напряжений σ_z от каждой силы по формуле

σ_z = k₁ Р₁ + k₂ Р₂+ k₃ Р₃ +… k_i Р_i = ∑ k_i Р_i, (2.3)

где k₁, k_2, k₃… k_i – коэффициенты, принимаемые в зависимости от r_i / z по табл. 2.1.

r₁, r₂, r₃…r_i – расстояния от точки М до сил соответственно Р₁, Р₂, Р₃…Р_i.

Вертикальных сил может быть сколь угодно. Величины сил и расстояния от них до точки М могут быть одинаковыми или разными. Данный случай определения напряжений принято называть метод элементарного суммирования. На практике он находит применение при загружении площадок произвольной формы и любом распределении передаваемого на грунт давления.

Задание 2.1.

Найти величину напряжений в точке М от сосредоточенных сил, расположенных как на рис. 2.2. Силы имеют одинаковую величину Р. Глубина расположения точки М, расстояния от неё до сил r_i указаны в табл. 2.2.

Величины напряжений σ_z при проведении вычислений находить с точностью до целых.

Таблица 2.2

Исходные данные для определения вертикального напряжения

Наименование показателей	Порядковый номер по заданию
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
	18	19	21	22	23	24	25	26	27	28	29	30
Сила Р, кН	12	21	16	18	11	24	13	29	19	27	21	15	28	14	31	20	32
Расстояния r, в м, r1 r2 r3 r4	0.5 1.1 1.5 1.1	0.7 1.4 2.0 0.7	1.0 1.8 2.8 2.8	0.4 0.8 1.4 0.8	0.9 1.2 1.8 1.8	1.1 1.8 2.2 1.8	0.4 1.7 2.8 1.7	0.4 1.6 2.4 1.6	1.2 1.9 2.3 1.2	0.8 1.8 3.6 3.6	1.3 2.1 3.1 3.1	0.3 1.3 1.7 0.3	1.0 1.5 2.6 2.6	1.1 1.9 2.9 1.9	0.9 2.4 3.5 3.5	1.2 2.0 3.0 3.0	08 2.3 2.9 2.9
Глубина z, в м	2	4	3	1.4	1.8	2.2	2.8	4.1	2.3	4.5	3.5	1.7	2.9	3.1	3.7	3.0	3.1

Пример 2.1.

Определить напряжение в точке от сосредоточенных сил, показанных на рис. 2.3.

Напряжение от силы Р₁ = 11 кН, r₁ = 0.

При r_{1 /} z = 0 по табл. .2.1 k₁ = 0.4775.

σ_z1 = 0.4775×11 = 5.25 кПа.

Напряжение от силы Р₂ = 7 кН; r₂ = 1.5 м.

r₂ / z = 1.5 /2.1 = 0.714. k₂ = 0.17.

σ_z2 = 0.17×7 = 1.19 кПа.

Напряжение от силы Р₃ = 9 кН; r₃ = 2.1 м.

r₃ / z = 2.1 /2.1 = 1, k₂ = 0.0844.

σ_z3 = 0.0844×9 = 0.76 кПа.

Напряжения от силы Р₄ = 13 кН; r₄ = 1.4 м.

r₄ / z = 1.4 /2.1 = 0.666, k4 = 0.191. σ_z4 = 0.191×13 =2.48 кПа.

σ_zм = 5.25+1.19+0.76+2.48 = 9.68 кПа.

2.2 Напряжения от равномерно распределенного давления.

Т акой вид нагрузки на грунты принимается в инженерных расчетах осадки фундаментов. Загруженная площадка имеет прямоугольную форму (рис. 2.4).

Для обозначения размеров и нагрузок на рис. 2.4 общеприняты следующие обозначения:

z – глубина расположения точки М от поверхности;

b – ширина загруженной площади, за которую всегда принимается наименьшая сторона;

l – длина загруженной площади, за которую всегда принимается наибольшая сторона;

p – нагрузка на единицу площади (интенсивность давления).

Интегрирование выражения для сосредоточенной силы по всей загруженной площади позволило получить выражение для определения вертикальных напряжений σ_z, в которое входят размеры сторон и интенсивность нагрузки p. Для произвольно взятых точек выражение имеет сложный вид и неудобно при проведении вычислений. В случаях, когда точки находятся под центром М и под углами М_у (на рис. 2.2 точка М_у показана под одним углом) прямоугольной площади, формулы приведены к виду, пригодному для практического использования.

Напряжения на любой глубине под центром площадки вычисляют по формуле:

σ_z = α p (2.4)

где α – коэффициент рассеивания напряжений, принимаемый по табл. 2.3 в зависимости от соотношения сторон подошвы  =l/b и относительной глубины расположения точки =2z/b.

Формула для определения напряжений под углом площадки в точке М_у имеет вид:

σ_zу= α_у p/4, (2.5)

где α_у - коэффициент рассеивания напряжений, принимаемый по табл. 2.3 в зависимости от соотношения сторон подошвы  =l/b и относительной глубины расположения точки _у=z/b.

Таблица 2.3

Величины коэффициента α

 = 2z/b у.= z/b	Коэффициент  для фундаментов
	Круглых	Прямоугольных с соотношением сторон  =l/b						Ленточных
		1	1,4	1,8	2,4	3,2	5
0	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000
0,4	0,949	0,960	0,972	0,975	0,976	0,977	0,977	0,977
0,8	0,756	0,800	0,848	0,866	0,876	0,879	0,881	0,881
1,2	0,547	0,606	0,682	0,717	0,739	0,749	0,754	0,755
1,6	0,390	0,449	0,532	0,578	0,612	0,629	0,639	0,642
2,0	0,285	0,336	0,414	0,463	0,505	0,530	0,545	0,550
2,4	0,214	0,257	0,325	0,374	0,419	0,449	0,470	0,477
2,8	0,165	0,201	0,260	0,304	0,349	0,383	0,410	0,420
3,2	0,130	0,160	0,210	0,251	0,294	0,329	0,360	0,374
3,6	0,106	0,131	0,173	0,209	0,250	0,285	0,319	0,337
4,0	0,087	0,108	0,145	0,176	0,214	0,248	0,285	0,306
4,4	0,073	0,091	0,123	0,150	0,185	0,218	0,255	0,28
4,8	0,062	0,077	0,105	0,130	0,161	0,192	0,230	0,258
5,2	0,053	0,067	0,091	0,113	0,141	0,170	0,208	0,239
5,6	0,046	0,058	0,079	0,099	0,124	0,152	0,189	0,223
6,0	0,040	0,051	0,070	0,087	0,110	0,136	0,173	0,208
6,4	0,036	0,045	0,062	0,077	0,099	0,122	0,158	0,196
6,8	0,031	0,040	0,055	0,064	0,088	0,110	0,145	0,185
7,2	0,028	0,036	0,049	0,062	0,080	0,100	0,133	0,175
7,6	0,024	0,032	0,044	0,056	0,072	0,091	0,123	0,166
8,0	0,022	0,029	0,040	0,051	0,066	0,084	0,113	0,158
8,4	0,021	0,026	0,037	0,046	0,060	0,077	0,105	0,150
8,8	0,019	0,024	0,033	0,042	0,055	0,071	0,098	0,143
9,2	0,017	0,022	0,031	0,039	0,051	0,065	0,091	0,137
9,6	0,016	0,020	0,028	0,036	0,047	0,060	0,085	0,132
10,0	0,015	0,019	0,026	0,033	0,043	0,056	0,079	0,126
10,4	0,014	0,017	0,024	0,031	0,040	0,052	0,074	0,122
10,8	0,013	0,016	0,022	0,029	0,037	0,049	0,069	0,117
11,2	0,012	0,015	0,021	0,027	0,035	0,045	0,065	0,113
11,6	0,011	0,014	0,020	0,025	0,033	0,042	0,061	0,109
12,0	0,010	0,013	0,018	0,023	0,031	0,040	0,058	0,106

Решение для определения напряжений под углом площадки позволяет находить напряжения в точках, расположенных в любом месте. Данный прием принято называть методом угловых точек. Сущность метода состоит в том, что загруженная площадка разделяется на участки, для каждого из которых точка М становится угловой М_у. Различные случаи местоположения точки М показаны на рис. 2.5. Напряжения в угловой точке от загружения каждого участка определяют по формуле (2.5). Полное напряжение в точке М равно сумме угловых напряжений от загружения каждого участка.

Задание 2.2.

Содержание задания.

1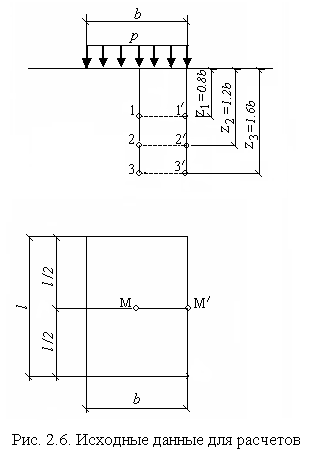 . вычислить нормальные напряжения σ_z от равномерно распределенной нагрузки (рис.2.6):

в точках 1, 2 и 3 под центром площадки;

в точках 1´, 2´ и 3´ под серединой длинной стороны методом угловых точек;

2. построить эпюры напряжений σ_z по вертикальным осям 1 – 3 и 1´ - 3´;

3. построить эпюры напряжений σ_z по горизонтальным осям 1 - 1´, 2 - 2´ и 3 - 3´;

4. оценить равномерность распределения напряжений σ_z по горизонтальным сечениям грунтового столба под загруженной площадкой.

5. разработать способы вычисления напряжений в точке М для случаев б, в и г рис. 2.5.

Исходные данные для проведения расчетов принять из табл. 2.4.

Таблица 2.4

Исходные данные для выполнения задания.

Значения параметров	Номер по заданию
	1	2	3	4	5		6	7		8	9		10
	11	12	13	14	15		16	17		18	19		20
Размеры площадки, в м ширина b	1,8	2,4	2,7	2,1	1,5		3	2,7		2,4	1,8		1,2
	2,4	2,7	3,0	2,4	2,1		2,4	1,8		1,5	2,1		2,4
длина l	2,4	3,3	3,9	3,6		2,4	3		4,5	2,7		3,3	1,8
	3,0	3,6	4,2	2,4		3,0	3,9		3,0	2,7		3,9	3,0
Давление на грунт р, в кПа,	290 240	310 280	220 300	360 260	300 320		370 200	240 340		330 230	410 290		300 380

Пример 2.2.

Определить напряжение σ_z в точке 2 под центром площадки (рис. 2.6), загруженной равномерно распределенной нагрузкой, при следующих данных:

l = 4.2 м, b = 2.4 м, z=1.2b, p = 320 кПа.

z = 1.2 ×2.4 = 2.88 м, =2z/b = 2×2.88 / 2.4 = 2.4,  = l/b = 4.2 / 2.4 =1.75.

По табл. 2.3 при  = 2.4 и  = 1.75 α = 0.371.

σ_z = α p = 0.371×320 = 118.72 кПа.

Пример 2.3.

П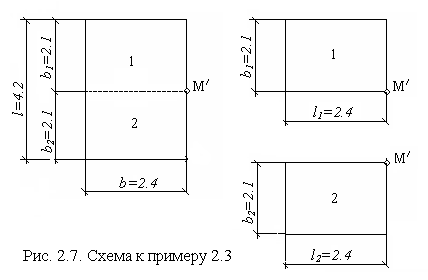 о данным примера 2.2 определить напряжение σ_z в точке 2´ под серединой длинной стороны площадки (рис. 2.6). Расчетная схема для определения показана на рис. 2.7.

Напряжения в точке 2´ определяются методом угловых точек. Через точку М´ проводим горизонтальную прямую, посредством которой загруженная площадка разделяется на два, в данном случае одинаковых, участка 1 и 2 длиной l₁=l₂=2.4 м шириной b₁=b₂= 2.1 м.. Для каждого из них М´ является угловой. Напряжения в находящейся под ней на глубине z = 2.88 м точке 2´ от загружения каждого участка определяется по формуле (2.5 ).

_у=z/b₁ = z/b₂= 2.88 / 2.1 = 1.37.

 = l₁/b₁ = l₂/b₂ = 2.4 / 2.1 = 1.14.

По табл. 2.3 при _у=1.37 и =1.14

α_у1= α_у2= 0 .685. σ_z2´ = α_у1 p/4+ α_у2 p/4 = 0685×320/4 + 0685×320/4 = 109.6 кПа.

Вопросы для самопроверки.

1. Какая нагрузка на грунт является самой простой?

2. Каким образом распределенную нагрузку на грунт можно заменить сосредоточенными силами?

3. Какие свойства приняты для идеализированного грунта?

4. На основе какого наблюдения задается распределение напряжений в грунтовом массиве от сосредоточенной силы на его поверхности?

5. Как определяют вертикальные напряжения σ_z под центром и σ_zу под углами прямоугольной площадки, загруженной равномерно распределенной нагрузкой?

6. Как определяют напряжения в грунтовом массиве методом угловых точек?

7. Как распределяются напряжения в грунтовом массиве под загруженной равномерно распределенной нагрузкой прямоугольной площадкой?

8. Как определяют напряжения в грунтовом массиве от собственного веса грунтов?