5. Перевірка статистичної гіпотези про відповідність емпіричного розподілу закону розподілу Пуассона

На рівні значущості α = 0,95 потрібно перевірити статистичну гіпотезу Н₀ про відповідність ряду кількості днів з опадами >10 мм на добу в червні на ст. Одеса (порт) даному теоретичному розподілу. Якщо гіпотеза Н₀ не відхиляється, записати основне рівняння розподілу Пуассона, враховуючи статистичні оцінки параметрів цього розподілу.

Використовуючи загальні теоретичні положення щодо перевірки статистичних гіпотез, розрахуємо "критерій згоди" Пірсона χ² за допомогою формули 4.13, а потім порівняємо його з критичним значенням цього критерію.

Розрахунки критерію Пірсона χ² наводяться в табл. 5.

Таблиця 5 – Порядок обчислення критерію Пірсона χ² на основі ряду кількості днів з опадами >10 мм на добу в червні на ст. Одеса (порт)

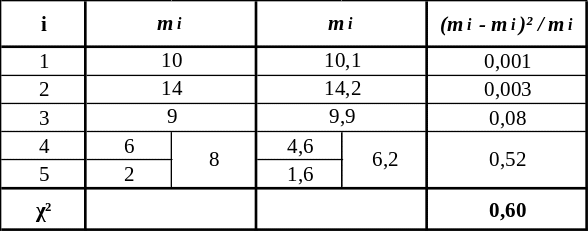
Як випливає з табл. 5, не всі 5 градацій вибірки є статистично забезпеченими. Тому необхідно об'єднати інтервальні частоти в тих градаціях, де m_i < 5. Це приводить до зменшення кількості часткових інтервалів до 4. Число ступенів вільності в нашому прикладі отримаємо таким чином: ν = k΄– 2 = 4 – 2 = 2.

З додатку М маємо: χ² (α, ν) = χ² (0,95; 2) = 0,103. Звідки випливає, що χ² > χ² (α, ν). Це говорить про прийняття гіпотези Н₁ – теоретичний розподіл, який вибрано для апроксимації ряду кількості днів з опадами >10 мм на добу в червні на ст. Одеса (порт), не відповідає йому. Проте гіпотеза Н₀ із ймовірністю 70 % приймається (при α = 0,70 χ² (0,70; 2) = 0,713, тобто χ² < χ² (α, ν)). Тому даний ряд можна апроксимувати розподілом Пуассона. Основне рівняння отриманого теоретичного закону має вигляд:

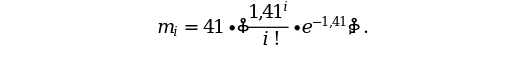
Cтатистична оцінка параметра розподілу Пуассона: λ = х = 1,41, а S_x = 1,35.

7