Міністерство освіти і науки, молоді та спорту України

Дніпропетровський національний університет імені Олеся Гончара

Геолого-географічний факультет

Кафедра гідрометеорології та геоекології

Практична робота №8

з дисципліни „Методи обробки, аналізу гідрометеорологічної інформації”

на тему: „ Перевірка статистичної гіпотези про відповідність емпіричного розподілу теоретичному ”

Виконала:

студентка групи ГМ-09

Зеркаль Анастасія

Перевірила:

к.т.н., доц.

Охотник К.К.

м. Дніпропетровськ

2013 р.

Перевірка статистичної гіпотези про відповідність емпіричного розподілу теоретичному

1. Перевірка статистичної гіпотези про відповідність емпіричного розподілу нормальному закону

У практичній роботі № 3 (табл. 9) для емпіричних інтервальних частот m_i були отримані відповідні теоретичні частоти нормального розподілу m_i (і = 1,10). Треба на рівні значущості α = 0,95 перевірити гіпотезу Н₀ про відповідність емпіричного розподілу середньодобової температури повітря на ст. Одеса нормальному закону. Для перевірки гіпотези Н₀ необхідно використати критерій Пірсона χ², який розраховується за формулою:

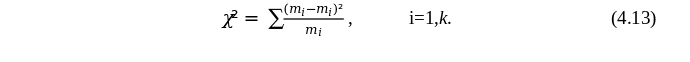Якщо гіпотеза Н₀ є вірною, записати в аналітичному вигляді отриманий теоретичний розподіл, враховуючи статистичні оцінки його параметрів.

Розрахунки критерію Пірсона χ² наводяться в табл. 1.

Таблиця 1 – Порядок обчислення критерію Пірсона χ² на основі статистичного ряду середньодобової температури повітря (ст. Одеса, 11 вересня)

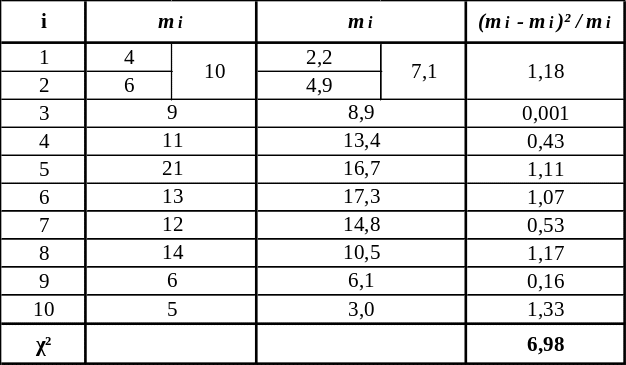
За умови нормального розподілу число ступенів вільності розраховується за допомогою рівняння: ν = k΄– 3.

Оскільки після об'єднання інтервальних частот на краях розподілу кількість статистично забезпечених часткових інтервалів зменшилася до 9, то маємо: ν = 9 – 3 = 6.

За додатком М знаходимо критичне значення параметра χ², яке залежить від рівня значущості (у нашому прикладі α = 0,95) і числа ступенів вільності ν, яке дорівнює 6.

Таким чином, χ² (0,95; 6) = 1,64, отже, χ² > χ² (α, ν), тому приймається гіпотеза Н₁; це означає, що теоретичний розподіл, який вибрано для апроксимації емпіричного розподілу, із заданою ймовірністю не відповідає останньому. У противному випадку гіпотеза Н₀ про відповідність емпіричного розподілу нормальному закону не відкидається на рівні значущості α = 0,30 ( χ² (0,30; 6) = 7,23, звідки χ² < χ² (α, ν)), а це означає, що із ймовірністю лише 30 % середньодобова температура повітря на ст. Одеса апроксимується нормальним законом.

Отриманий для даного емпіричного розподілу теоретичний закон описується щільністю ймовірності f(x) нормального розподілу:

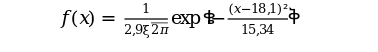
та функцією розподілу F(x) цього закону:

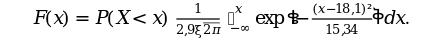
Статистичні оцінки параметрів масштабу та форми нормального розподілу відповідно дорівнюють:

m_x = x = 18,1 °C;

σ_x → S_x = 2,77 °C.

Зважаючи на те, що емпіричний розподіл середньодобової температури повітря апроксимується із ймовірністю 30 %, до нього доцільно підібрати інший теоретичний закон.

2. Перевірка статистичної гіпотези про відповідність емпіричного розподілу

I типу розподілів Пірсона

При розв'язанні типової задачі для емпіричних інтервальних частот m_i були отримані відповідні теоретичні частоти m_i (і = 1,12) І типу розподілів Пірсона. Вони знаходяться в табл. 11 (3-й та 9-й стовпчики) та в табл. 2.

Треба за допомогою критерію Пірсона χ² на рівні значущості α = 0,95 перевірити гіпотезу Н₀ про відповідність емпіричного розподілу швидкості вітру на ст. Одеса першому типу розподілів Пірсона. Якщо гіпотеза Н₀ є вірною, записати основне рівняння І типу розподілів Пірсона, враховуючи статистичні оцінки параметрів цього закону.

Використовуючи загальні теоретичні положення щодо перевірки статистичних гіпотез, розрахуємо "критерій згоди" Пірсона χ² за допомогою формули 4.13, а потім порівняємо його з критичним значенням цього критерію.

Розрахунки критерію Пірсона χ² наводяться в табл. 2.

Таблиця 2 – Порядок обчислення критерію Пірсона χ² на основі статистичного ряду швидкості вітру (ст. Одеса)

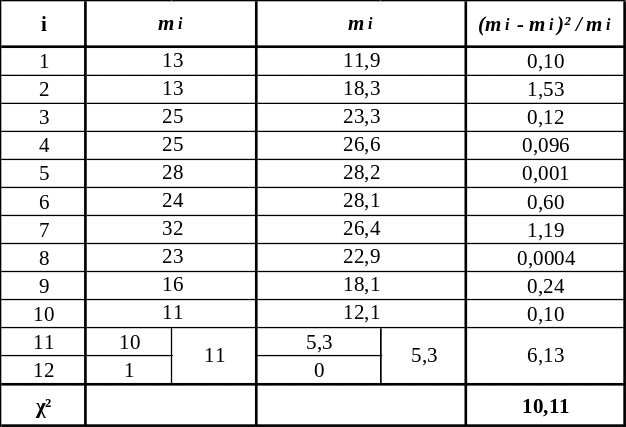
Як випливає з табл. 19, не всі 12 градацій вибірки є статистично забезпеченими. Тому необхідно ліквідувати цей недолік і об'єднати інтервальні емпіричні частоти в тих градаціях, де m_i < 5 (одинадцяту з дванадцятою). Це приводить до зменшення кількості часткових інтервалів до 11. Число ступенів вільності в нашому прикладі отримаємо таким чином: ν = k΄– 5 = 11 – 5 = 6.

З додатку М знаходимо: χ² (α, ν) = χ² (0,95; 6) = 1,64.

Оскільки χ² > χ² (α, ν), приймається гіпотеза Н₁, тому теоретичний розподіл із ймовірністю 95 % не може бути вибраний для апроксимації емпіричного розподілу швидкості вітру на ст. Одеса. Гіпотеза Н₀ може бути прийнята на рівні значущості α = 0,10 (із ймовірністю лише 10 %).

Статистичні оцінки параметрів І типу розподілів Пірсона дорівнюють:

m₀ = 28,41; q₁ = 1,16; q₂ = 1,23; l₁ = 6,09; l₂ = 6,46.

За умови можливості апроксимації емпіричного розподілу швидкості вітру І типом розподілів Пірсона відповідно отриманих оцінок параметрів його основне рівняння мало б вигляд:

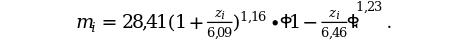
Отже, для апроксимації даного емпіричного розподілу зі значно більшою ймовірністю необхідно шукати інший теоретичний закон.