Определение поправок или корректировок

После сопоставления и выявления всех факторов различия оценщик должен внести поправки в стоимость объектов-аналогов. Следует специально подчеркнуть, что все поправки относятся к аналогам, а не к объекту оценки.

Целесообразна следующая очередность внесения поправок:

 поправки на техническую сопоставимость;

 поправки к ценам на различия в условиях продажи.

Среди поправок на техническую сопоставимость различают поправки:

 на типоразмер (мощность, грузоподъемность, производительность);

 комплектацию (наличие дополнительных приспособлений и устройств);

 возраст;

 качество;

 состояние, степень физического износа;

 местоположение объекта при продаже (на месте его использования, на складе дилера).

На практике подобранные аналоги часто отличаются по мощности, производительности от объекта оценки. В этом случае для определения поправки используются соотношения между ценами (затратами на изготовление) и параметрами машин, в частности степенная зависимость:

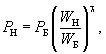
где Р_Н, Р_Б  цены (затраты) новой и базовой машины (аналога);

W_Н, W_Б  мощность, производительность или иной параметр сопоставимых машин;

  показатель степени, часто называемый коэффициентом «торможения цены», зависящий от конкретного вида технических устройств.

Значения показателя степени  определены для ряда изделий машиностроения на основе специальных исследований, а также многолетней практики.

Приведенная формула широко используется из-за ее простоты и достаточно высокой надежности. Вместе с тем надо учитывать, что зависимости между ценами и параметрами имеют в действительности более сложный характер, чем это определяется формулой. Так, для тракторов средней мощности используется значение , равное 0,72, для экскаваторов  0,8, для экструдеров, применяемых в переработке полимерных материалов  0,60,7 и т. д.¹

В связи с этим значение показателя степени , как правило, не может быть принято одинаковым для всего диапазона значений одного и того же параметра.

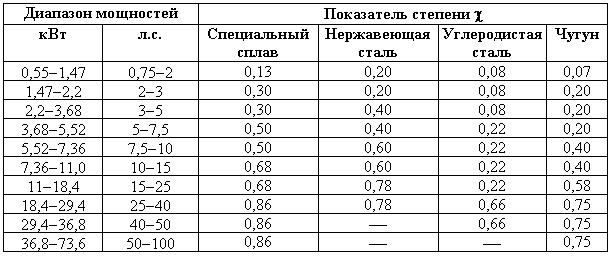
Например, для горизонтальных центробежных насосов, изготовленных из различных материалов, в таблице 13.6 даны значения показателя степени  в зависимости от диапазона мощности.

Очевидно, что формулой можно пользоваться только для сопоставления машин с близкими значениями параметров (для машин из однородной группы), иначе точность результата резко снижается.

Таблица 13.6

Значения показателя степени  для горизонтальных центробежных насосов

Обычно считается, что различия в параметрах не должны превышать 3050%. Ниже приведены значения показателя степени  по различным источникам (табл. 13.7).

Таблица 13.7

Значения показателя степени  для транспортеров

Примечание. Если размеры выражены в миллиметрах, то их произведение нужно разделить на 7750.

Для ленточных транспортеров длина умножается на ширину, для шнековых транспортеров длина умножается на диаметр. Для шнековых питателей значения  такие же².

Значения показателя степени  для различных технических устройств приведены в табл. 13.8.

Таблица 13.8

Значения показателя степени 

В таблицах 13.913.10 приведены некоторые поправки, связанные с различием в частоте вращения, для устройств, относящихся к различным отраслям техники.

Таблица 13.9

Поправки на частоту вращения электродвигателей

Таблица 13.10

Поправки на частоту вращения двигателей внутреннего сгорания

При наличии нескольких параметров, каждый из которых достаточно сильно влияет на затраты при производстве машины и, следовательно, на цены, необходимо применять более сложные математические зависимости.

Обычно для этого используют модели цен. Они представляют собой математические выражения, связывающие цены и параметры изделий. Имея такое выражение и подставляя в него значения параметров конкретного изделия, можно получить его цену.

Для построения параметрических моделей цен наиболее широко используется метод корреляционно-регрессионного анализа.

В общем виде зависимость цены изделия от его параметров выглядит так:

P  f(x₁, x₂, ... x_k : a₀, ... a_k),

где Р  цена изделия;

х₁, ..., х_k  параметры,

а₀, а₁, … а_k  коэффициенты.

Задача заключается в том, чтобы найти математическое выражение путем обработки имеющейся информации о ценах и параметрах однотипных изделий. Последовательность действий при построении математической модели регрессионного типа такова:

 выбор параметров изделия на основе парных коэффициентов корреляции, в наибольшей степени влияющих на уровень цены, но не имеющих между собой высокие парные коэффициенты корреляции для устранения мультиколлинеарности;

 выбор формы зависимости  выбор вида уравнения регрессии³;

 формирование массива исходной информации;

 выполнение математических процедур (определение коэффициентов уравнения регрессии с оценкой погрешности расчета коэффициентов и уровня значимости их);

 анализ полученных результатов и выбор окончательного варианта модели по наименьшей дисперсии (или корреляционного отношения).

Чаще всего используют два вида формул (из-за простоты вычислений параметров).

Линейная формула Р  а₀  а₁х₁  а₂х₂  ...  а_mх_m,

где a₁, ... а_m  коэффициенты параметрического уравнения;

а₀  свободный член.

^{Степенная мультипликативная формула}

Например, линейный вид функции был использован при построении параметрических моделей цен металлорежущих станков фирм ФРГ и США для исследования их сравнительной конкурентоспособности.

Цена станков фирмы «Нью Геркулес» была выражена линейной моделью следующего вида:

у  55,2x₁  0,98x₂  2,37х₃  1510х₄  14 657,

где у  цена станка, дол.;

x₁  наибольший диаметр обрабатываемого изделия, мм;

x₂  расстояние между центрами, мм;

х₃  максимальная частота вращения шпинделя, об./мин;

х₄  мощность электродвигателя, л. с.