Билет №14

1. Билет 12

Биссектриса угла — геометрическое место точек внутри угла, равноудалённых от сторон угла.

1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон

2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

3. Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.

4. Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.

5. Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.

6. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).

7. Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора.

Билет №15

Билет №8

Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым.

Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180° ( радиан).

Можно описать окружность около:

любого прямоугольника (частный случай квадрат)

любой равнобедренной трапеции

любого четырехугольника, у которого сумма противоположных углов равна 180 градусов

У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон:

|AC|·|BD| = |AB|·|CD| + |BC|·|AD|

Билет №16

S= AB * KH

Билет №17

S	=	1	d1d2 sinα
		2

Билет №10

S	=	a + b	h
		2

S = hm

S	=	4r2
		sinα

Вектор в геометрии — класс коллинеарно направленных отрезков.

Операцию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый из которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и геометрически фундаментальное, удобно для сложения любого количества векторов, однако правило параллелограмма более удобно для фиксированных или скользящих векторов, так как не требует переноса второго слагаемого (что в принципе могло бы смущать или запутывать в этих случаях) для построения суммы, то есть удобно для сложения векторов с началом в одной точке, в добавок имея то преимущество, что в нем более очевидно равноправие слагаемых; координатное же определение, являясь простым и удобным, бывает очень полезно для вычислений.

Пример 1. Найти произведение вектора 

a = {1;2}на 3.   Решение 

3 · a ={3 · 1; 3 · 2} = {3; 6}

Билет №18

Билет №17

Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.

Билет №19

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.

Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Два треугольника подобны,  если  три  стороны одного треугольника пропорциональны трём сторонам другого треугольника.

Пусть в треугольниках ABC и А'В'С  / A = / А' ;  / В = / B'. ¹ Доказать, что /\ АВС   /\ А'В'С (черт. 367).

Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. / C = / С'.

Отложим от вершины В, например, на стороне АВ треугольника ABC отрезок ВМ, равный отрезку А'В'. Из точки М проведём прямую MN || АС. Мы получили/\ MBN, который подобен /\ ABC. Но /\ MBN = /\ А'В'С', так как / В =/ В' по условию теоремы; сторона MB = A'B' по построению; / BMN = / A' (/ BMN и / А' порознь равны одному и тому же / А).

Если /\ MBN   /\ AВС, то /\ А'В'С'   /\  ABC. Эта теорема выражает  1-й признак подобия треугольников.

В случае n=3 смотреть Теорема о сумме углов треугольника.

Пусть   — данный выпуклый многоугольник и n > 3. Тогда проведем из одной вершины к противоположным вершинам n-3 диагонали: . Так как многоугольник выпуклый, то эти диагонали разбивают его на n — 2 треугольника:  . Сумма углов многоугольника совпадает с суммой углов всех этих треугольников. Сумма углов в каждом треугольнике равна 180°, а число этих треугольников есть n-2. Следовательно, сумма углов n-угольника равна 180°(n-2). Теорема доказана.

Билет №20

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

или

A x + B y + C = 0

y = k x + b

Билет №21

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.

Теорема о средней линии трапеции:

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Билет №22

Серединный перпендикуляр — прямая, перпендикулярная к данному отрезку и делящая его на две равные части.

• Серединные перпендикуляры к сторонам треугольника (или другого описываемого окружностью многоугольника) пересекаются в одной точке — центре описанной окружности.

• Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Билет №23

Любой вектор р можно разложить, и притом единственным образом, по двум данным неколлинеарным векторам а и b р=ха=yb

S =	1	a · h
	2

S =

S =	1	a · b · sin γ
	2

S = 

S = p · r

Билет №24

Теорема синусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами.

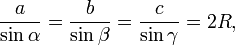
Билет №25