Билет №11

Сумма углов треугольника всегда равна 180°.

Теорема о внешнем угле треугольника:

Внешний угол треугольника всегда равен сумме углов не смежных с ним.

Формула Эйлера:  , где   — радиус описанной вокруг треугольника окружности,   — радиус вписанной в него окружности, O — центр описанной окружности, I — центр вписанной окружности.

• Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.

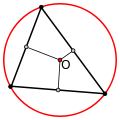
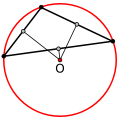
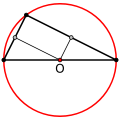
• У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.

• 

Остроугольный

 

• 

Тупоугольный

 

• 

Прямоугольный

Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.

• 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.

• Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.

• Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

Радиус

Радиус описанной окружности может быть найден по формулам

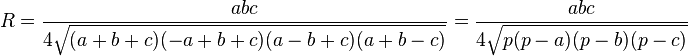
Билет №12

Прямоугольник — параллелограмм, у которого все углы прямые.

• Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны.

• Стороны прямоугольника являются его высотами.

• Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).

• Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).

Параллелограмм является прямоугольником, если выполняется любое из условий:

• Если диагонали параллелограмма равны.

• Если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон.

• Если углы параллелограмма равны.

Билет №13

Ромб – это параллелограмм, у которого все стороны равны.

1. Ромб является параллелограммом. Его противолежащие стороны попарно параллельны, АВ || CD, AD || ВС.

2. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам.

3. Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны между собой.

Формула для нахождения угла выглядит вот так:

.

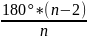
r = R cos