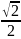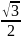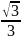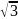Билет №1

1. Вертикальные углы – это углы, стороны которых продолжают друг друга.

Смежные углы – это пара углов, которые дополняют друг друга до 180 градусов.

Свойства вертикальных углов:

1) Вертикальные углы равны.

2) Вертикальные углы располагаются на продолжении сторон друг друга.

Свойства смежных углов:

1. Сумма смежных углов всегда равна 180 градусам.

2. У смежных углов общая вершина.

3. У смежных углов одна сторона общая.

4. Другие стороны лежат на одной прямой, не совпадая.

2. Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе треугольника.

Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе треугольника.

Тангенс острого угла прямоугольного треугольника – это отношение прилежащего катета к противолежащему.

Котангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему.

Д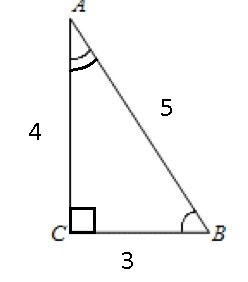 оказательство основного тригонометрического тождества.

Синус данного треугольника равен .

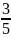Косинус данного треугольника равен .

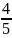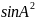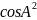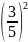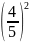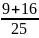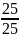+ =1

+ =1 =1 =1 1=1

Что и требовалось доказать.

3. Задача по теореме «уравнение окружности»

Длина окружности:

Радиус окружности:

Диаметр окружности:

Площадь круга радиуса R:

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:

Билет №2

1. Равные треугольники – это треугольники, которые при наложении будут полностью совпадать.

Первый признак равенства треугольников:

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников:

Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников:

Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Доказательство первого признака равенства треугольников:

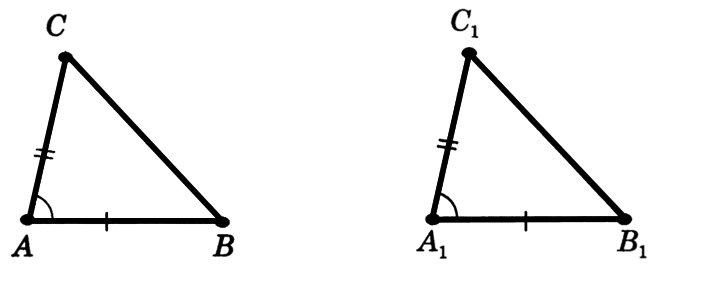
Рассмотрим ∆ ABC и ∆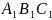 , у которых AC = 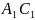, AB = 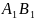, угол A и 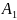равны. Докажем, что ∆ABC = ∆ .

Так как ∠A=∠ , то треугольник ABC можно наложить на треугольник так, что вершина A совместится с вершиной . Поскольку AB = , AC = , то сторона AB совместится со стороной , а сторона AC - со стороной ; в частности совместятся точки B и ,

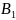C и 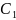. Следовательно, совместятся точки BC и 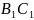. Итак, треугольники

ABC и полностью совместятся, значит, они равны.

2. Смотри Билет №1 вопрос 2

α	30°	45°	60°
Sin A
Cos A
Tg A		1

Билет №3

1. Равнобедренный треугольник – это треугольник, в котором боковые стороны равны между собой по длине.

Свойства углов при основании равнобедренного треугольника:

• Углы, лежащие напротив равных сторон равнобедренного треугольника, межу собой равны.

• Так же равны биссектрисы, медианы и высоты, проведенные из этих углов.

• Биссектриса, проведенная к основанию равнобедренного треугольника, совпадает с медианой, высотой и серединным перпендикуляром.

Билет №4

Вписанный угол – это угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.

Теорема о вписанном угле:

Вписанный угол измеряется половиной дуги, на которую он опирается.

Доказательство:

Пусть ∠ABC = α. Тогда:

1. ∠B = ∠A = α (OA=OB=R)

2. ∠AOC = 2α (Внешний угол)

Следовательно:

∠B = α = ∠AOC = дуги AC

Билет №5

Е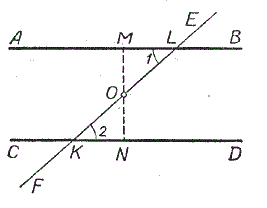 сли при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны.

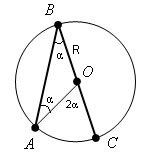
Пусть прямые АВ и CD пересечены прямой EF и ∠ 1 = ∠2. Возьмём точку О — середину отрезка КL секущей ЕF. Опустим из точки О перпендикуляр ОМ на прямую АВ и продолжим его до пересечения с прямой СD, АВ_|_МN. Докажем, что и СD_|_МN.

Для этого рассмотрим два треугольника: МОЕ и NОК. Эти треугольники равны между собой. В самом деле: ∠1 = ∠ 2 по условию теоремы; ОK = ОL — по построению;

∠МОL = ∠NОК, как вертикальные углы. Таким образом, сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника; следовательно, ∆ МОL = ∆ NОК, а отсюда и

∠ LМО = ∠ КNО, но LМО прямой, значит, и ∠КNО тоже прямой. Таким образом, прямые АВ и СD перпендикулярны к одной и той же прямой МN, следовательно, они параллельны, что и требовалось доказать.

Если при пересечении 2-х прямых секущей, прямые параллельны, то накрест лежащие углы равны.

Билет №6

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Доказательство:

∠2 = ∠3 ( как вертикальные)

∠1 = ∠2 ( по условию)

Следовательно:

∠1 = ∠3

Но так, как эти углы накрест лежащие, то прямые параллельны по 1-ому признаку.

Если при пересечении 2-х прямых секущей, прямые параллельны, то накрест лежащие углы равны.

Медиана – отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.

Все три медианы треугольника пересекаются в одной точке.

П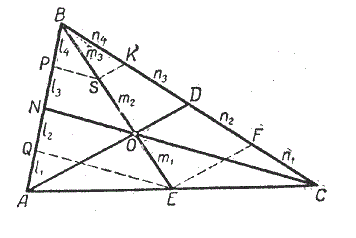 усть в треугольнике АBС АD и ВЕ — медианы, пересекающиеся в точке О. Докажем, что и отрезок NС, проходящий через третью вершину этого треугольника и точку О, будет также медианой, т. е. AN = NВ.

Для доказательства через точку Е проведём ЕF || АD, тогда СF = FD. Разделим отрезок ВD пополам; пусть DК = КВ. Получим п₁ = п₂ = п₃ = п₄, как половины равных отрезков СD и ВD.

Через точку K проведём KS || АD; тогда m₁ = m₂ = m₃, так как KS || ОD || ЕF и  п₄ = п₃ = п₂ .

Через точки S и Е проведём SP || ОN и EQ || ОN, тогда l₄ = l₃ = l₂, так как SР || ОN || ЕQ и m₃ = m₂ = m₁. Кроме того, l₂ = l₁, так как AE = ЕС и ЕQ || СN.  Отсюда l₄ = l₃ = l₂= l₁, но  l₄ + l₃ = NВ, а l₂+ l₁ = NA.

Следовательно, AN = NВ, т. е. NС является так же медианой треугольника AВС.

Таким образом, все три медианы треугольника пересекаются в одной точке.

Кроме того, мы видим, что отрезок ОЕ составляет ¹/₃ ВЕ. Аналогично можно доказать, что отрезок ON составляет ¹/₃ СN и отрезок OD составляет ¹/₃ AD. Таким образом, точка пересечения медиан в треугольнике отделяет от каждой медианы третью часть, считая от соответствующей стороны.

Билет №7

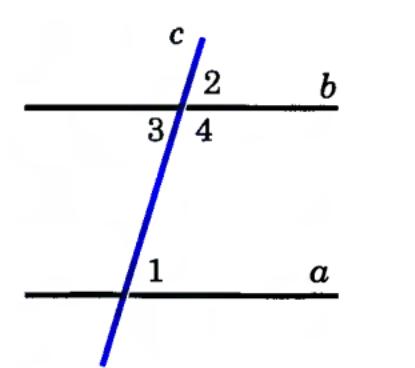
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Д оказательство:

3 +4 = 180°(как смежные)

1 +4 = 180°(по условию)

Следовательно:

1 = 3 (как накрест лежащие)

Поэтому a || b по 1-ому признаку.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и все углы между собой равны.

Площадь правильного многоугольника с числом сторон   и длиной стороны  составляет:

.

Площадь правильного многоугольника с числом сторон  , вписанного в окружность радиуса  , составляет:

.

Площадь правильного многоугольника с числом сторон  , описанного вокруг окружности радиуса  , составляет:

(площадь основания n-угольной правильной призмы)

Площадь правильного многоугольника с числом сторон   равна

,

где   — расстояние от середины стороны до центра,   — длина стороны.

Площадь правильного многоугольника через периметр ( ) и радиус вписанной окружности ( ) составляет:

.