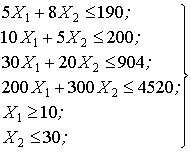Практическое задание

Логистическая концепция организации производства включает в себя следующие основные положения:

• отказ от избыточных запасов;

• сокращение времени выполнения основных и транспортно-складских операций;

• устранение простоев оборудования;

• устранение нерациональных внутрипроизводственных перевозок;

• улучшение качества продукции;

• отказ от изготовления продукции впрок при отсутствии заказов на нее.

2.2.1. Задача формирования производственной программы и управления запасами ресурсов

1. Постановка задачи и построение ее математической модели

2. Графический метод решения задачи оптимизации производственной программы

3. Графическое решение задачи с помощью Excel

4. Решение задачи линейного программирования симплексным методом

5. Анализ решения с помощью двойственного симплекс-метода

6. Аналитический метод решения с использованием программы Excel

7. Оптимизация запасов ресурсов в условиях узкой специализации работы предприятия

8. Пример решения задачи оптимизации запасов ресурсов в условиях узкой специализации производства

9. Исходные данные задачи формирования производственной программы

2.2.2. Оптимизация запуска деталей в обработку

1. Задача об одном станке

2. Задача о двух станках. Алгоритм Джонсона

3. Обобщения алгоритма Джонсона и рекомендации по составлению расписания

4. Построение графиков Ганта

5. Оптимизация работы оборудования путем концентрации его микропростоев

6. Исходные данные задачи оптимизации порядка запуска деталей в обработку

2.2.3. Задачи сетевого планирования комплекса работ

1. Пример решения задачи сетевого планирования комплекса работ

2. Исходные данные сетевого планирования комплекса работ

2.2.4. Задача о реконструкции предприятия

1. Метод динамического программирования

2. Пример решения задачи о реконструкции методом динамического программирования

2.2.1. Задача формирования производственной программы и управления запасами ресурсов

Данная задача в соответствии с логистическим подходом охватывает в единое целое проблемы и производственной логистики и логистики запасов. Ее решение одновременно позволяет существенно увеличить объем выпуска продукции и сократить затраты связанные приобретением и хранением запасов.

1. Постановка задачи и построение ее математической модели

Пусть, например, некоторое малое предприятие планирует выпуск двух видов продукции А и Б. Для этого имеется сырье двух видов, запасы которых приведены в таблице 2.2.1. В аренду взято 5 станков и принято на работу 20 рабочих. Известны нормы расхода всех видов ресурсов на каждый вид продукции и цена единицы каждого вида ресурсов (см. табл. 2.2.1).

Таблица 2.2.1

Исходные данные примера задачи оптимизации производственной программы и оптимизации запасов ресурсов
Наименование ресурса	Запас ресурса	Цена единицы ресурса	Нормы расхода ресурса на производство продукции вида
			А	Б
Сырье С1	190	20	5	8
Сырье С2	200	30	10	5
Станки	904	20	30	20
Труд. ресурсы	4520	10	150	200

Если считать, что число рабочих дней в году 226, то ресурс рабочего времени рабочих в нашем случае составит 5×226×0,8= 904 машинодня. Здесь 0,8 – коэффициент использования рабочего времени (станки нуждаются в перенастройке, замене инструмента, смазке, профилактическом ремонте). Ресурс рабочего времени рабочих определяется аналогично, при условии, что коэффициент использования рабочего времени равен единице и в данном случае – 20×226×1=4520 человеко-дней. В клетках «цена единицы продукции» указана стоимость одного машинодня работы станков и одного человеко-дня работы рабочих.

Прибыль от реализации единицы продукции первого вида составит 220 у.д.е., а от реализации единицы продукции второго вида составит 330 у.д.е.

В соответствии с уже заключенным договором продукции вида А необходимо произвести не менее 10 единиц.

Исследование рынка показало, что продукции вида Б можно реализовать в количестве не более 30 единиц.

Прибыль от реализации единицы продукции вида А составит 220 у.д.е., от реализации единицы продукции вида В – 330 у.д.е.

Необходимо определить количество продукции каждого вида, которое можно произвести при имеющихся запасах ресурсов с целью получения максимальной прибыли.

В качестве элементов решения примем Х₁ – количество продукции вида А; Х₂ – количество продукции вида Б, которое необходимо выпустить при имеющихся запасах сырья для получения максимальной прибыли.

В этом случае математическая модель будет иметь вид

(2.2.1)

Очевидно, что эта модель относится к классу задач линейного программирования (ЗЛП), а так как число неизвестных здесь равно двум, то она может быть решена не только аналитическим, но и графическим методом.