
- •4.1. Сущность распределительной логистики
- •4.2. Задачи распределительной логистики
- •4.3. Логистические каналы и цепи сбыта
- •4.4. Построение системы распределения
- •Построение распределенной системы управления автотранспортным предприятием.
- •5.1. Понятие распределительной логистики
- •5.2. Дистрибутивные каналы и сети
- •5.3. Логистические посредники в распределении
- •Практическое задание
- •2.2.1. Задача формирования производственной программы и управления запасами ресурсов
- •1. Постановка задачи и построение ее математической модели
- •2. Графический метод решения задачи оптимизации производственной программы
- •3. Графическое решение задачи с помощью Excel
- •4. Решение задачи линейного программирования симплексным методом
- •5. Анализ решения с помощью двойственного симплекс-метода
- •6. Аналитический метод решения с использованием программы Excel
- •7. Оптимизация запасов ресурсов в условиях узкой специализации работы предприятия
- •8. Пример решения задачи оптимизации запасов ресурсов в условиях узкой специализации производства
- •Оценка экономической эффективности решения задачи оптимизации запасов в условиях узкой специализации производства
- •9. Исходные данные задачи формирования производственной программы
- •Исходные данные задачи при использовании симплексного метода
- •Исходные данные задачи при использовании Excel
- •2.2.2. Оптимизация запуска деталей в обработку
- •1. Задача об одном станке
- •2. Задача о двух станках. Алгоритм Джонсона
- •3. Обобщения алгоритма Джонсона и рекомендации по составлению расписания
- •Обобщения алгоритма Джонсона
- •4. Построение графиков Ганта
- •5. Оптимизация работы оборудования путем концентрации его микропростоев
- •6. Исходные данные задачи оптимизации порядка запуска деталей в обработку
- •2.2.3. Задачи сетевого планирования комплекса работ
- •1. Пример решения задачи сетевого планирования комплекса работ
- •2. Исходные данные сетевого планирования комплекса работ
- •2.2.4. Задача о реконструкции предприятия
- •1. Метод динамического программирования
- •2. Пример решения задачи о реконструкции методом динамического программирования
- •Тест самоконтроля к теме 2.2. Производственная логистика
1. Пример решения задачи сетевого планирования комплекса работ
Построение сетевого графика начинается с простого перечисления всех необходимых работ (таблица 2.2.12).
Таблица 2.2.12
Пример организации исходных данных программирования задачи сетевого планирования |
||||
Наименование работы |
Обозначение работы |
Опирается на работу |
Ранг работы |
Новая нумерация |
Монтаж крана |
b1 |
b3, b6 |
3 |
a5 |
Закладка фундамента |
b2 |
b4, b5, b6 |
3 |
a6 |
Завоз оборудования |
b3 |
b5 |
2 |
a3 |
Завоз материалов |
b4 |
b5 |
2 |
a4 |
Расчистка территории |
b5 |
- |
1 |
a1 |
Разметка |
b6 |
b5 |
2 |
a2 |
Возведение стен |
b7 |
b1, b2, b4 |
4 |
a7 |
Монтаж перекрытия |
b8 |
b7 |
5 |
a8 |
Электротехнические работы |
b9 |
b8 |
6 |
a9 |
Сантехнические работы |
b10 |
b8 |
6 |
a10 |
Приемосдаточные испытания |
b11 |
b8, b9, b10 |
7 |
a11 |
Затем на основании простого логического анализа заполняется второй столбец таблицы и определяется ранг каждой работы. Работы первого ранга не опираются на другие. Работы второго ранга опираются только на работы первого ранга. Работы третьего ранга могут опираться на работы второго и первого ранга и т.д.
После этого производится перенумерация работ и заполняется последний столбец таблицы. При этом безразлично, в каком порядке присваивать номера работам одного и того же ранга.
После этого составляется новая таблица, в которой указывается продолжительность выполнения каждой работы (таблица 6.13).
Таблица 2.2.13
Упорядоченные исходные данные сетевого планирования |
|||
Наименование работы |
Обозначение работы |
Опирается на работу |
Продолжительность работы |
Расчистка территории |
a1 |
- |
6 |
Разметка |
a2 |
a1- |
2 |
Завоз оборудования |
a3 |
a1 |
4 |
Завоз материалов |
a4 |
a1 |
2 |
Монтаж крана |
a5 |
a2, a3 |
5 |
Закладка фундамента |
a6 |
a2, a4 |
3 |
Возведение стен |
a7 |
a4, a5, a6 |
7 |
Монтаж перекрытия |
a8 |
a7 |
6 |
Электротехнические работы |
a9 |
a8 |
3 |
Сантехнические работы |
a10 |
a8 |
5 |
Приемосдаточные испытания |
a11 |
a9, a10 |
6 |
Существует несколько методов решения задач сетевого планирования. По-видимому, наиболее наглядным и простым является графоаналитический метод. При этом методе сначала проводится ось времени. В начале оси располагается исходный узел 0. Величина стрелки и угол ее наклона для любой работы выбираются таким образом, чтобы ее проекция на ось времени была равна ее продолжительности. Очевидно, что в этом случае есть множество вариантов изображения каждой работы. Например, на рисунке 2.2.23 приведено три варианта изображения одной и той же работы.
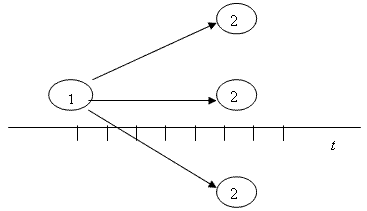 Рисунок
2.2.23 – Варианты изображения одной и той
же работы
Рисунок
2.2.23 – Варианты изображения одной и той
же работы
Если же одна работа опирается на несколько других, то изображающая ее стрелка должна начинаться из самого правого кружка, а логическая связь с другими работами изображается пунктирными стрелками (фиктивные работы). Пример этого случая приведен на рисунке 2.2.24.
 Рисунок
2.2.24 – Фрагмент временного сетевого
графика с фиктивными работами
Рисунок
2.2.24 – Фрагмент временного сетевого
графика с фиктивными работами
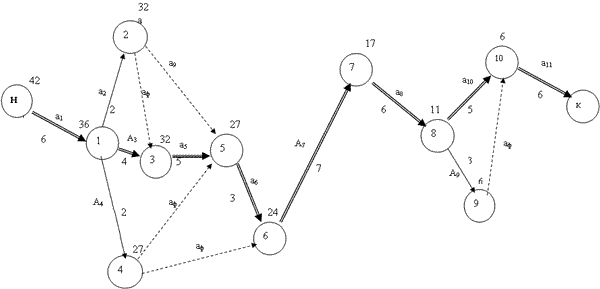
Сетевой график, построенный на основании исходных данных программирования таблицы 2.2.12, приведен на рисунке 2.2.25.
 Рисунок
2.2.25 – Сетевой график комплекса работ,
построенный графоаналитическим
методом
Рисунок
2.2.25 – Сетевой график комплекса работ,
построенный графоаналитическим
методом
На графике двойными стрелками выделены критические работы. Критическая дуга составляется только из сплошных стрелок. Из графика, построенного графоаналитическим методом сразу видна общая продолжительность производственного процесса. В данном случае Тобщ=42 дня.
Фиктивные работы характеризуют резервы времени соответствующих реальных работ. Эти резервы определяются проекцией соответствующей фиктивной работы на ось времени. В данном случае работа а2 имеет резерв времени в два дня, а4 – восемь дней, а9 – один день.
Знание этих резервов позволяет изменить сроки начала некритических работ и дать рекомендации о перераспределении имеющихся ресурсов в пользу критических работ с целью сокращения общей продолжительности выполнения всего комплекса.
Например, завоз оборудования можно осуществить не сразу после завершения работы а1, а на 8 дней позже (см. рис. 2.2.25). При этом не будет излишне загромождаться территория, и само оборудование будет более сохранным.
Если же, некоторые некритические работы выполняются за счет трудовых ресурсов, то вполне можно снять с них часть рабочих и перевести их на выполнение критических работ.
Задачам сетевого планирования характерны все свойства задач динамического программирования:
задача может быть разбита на этапы (по времени, в пространстве, этапы производственного процесса и пр.);
аддитивность решения – результат решения всей задачи может быть получен в результате суммирования результатов решения на каждом отдельном этапе;
регрессивность решения – решение разворачивается от конца к началу.
На рисунке 2.2.26 показано решение той же задачи методом динамического программирования.
 Рисунок
2.2.26 – Решение задачи сетевого планирования
методом динамического программирования
Рисунок
2.2.26 – Решение задачи сетевого планирования
методом динамического программирования
Вначале безо всяких масштабов строится сетевой график. Для определения продолжительности выполнения всего комплекса работ, в соответствии с принципами динамического программирования, процесс решения разворачивается от конца к началу.
В конечное состояние 11 система может перейти из состояния 10. Для этого потребуется 6 дней (а11=6).
В состояние 10 система может перейти из состояния 6, 9 и 8. Максимальное время этого перехода составляет 5 дней (работа а10). 9-10 и 6-10 – фиктивные работы, не требующие затрат времени, поэтому над кружками 9 и 10 ставим предыдущее число 6.
В состояние 8 система может перейти по дуге а2-а8, а3-а7, а4-а7, а3-а5 и а4-а5. Длины этих дуг (в днях) составляют, соответственно, – 20, 11, 9, 15 и 13 дней. Наибольшей продолжительности требует переход системы из 2 в 8, а все остальные состояния соединяем с 8 фиктивными работами (пунктирными стрелками). Аналогичным образом доходим до начала производственного процесса.
Окончательный результат, естественно, получается точно таким же, как и при использовании графоаналитического метода.
Использование различных методов при решении одной и той же задачи позволяет исключить возможность появления даже случайной ошибки и широко используется в научных исследованиях и в проектной практике.
