6. Исходные данные задачи оптимизации порядка запуска деталей в обработку

Исходные данные приведены в таблице 2.2.11

Таблица 2.2.11

Исходные данные
Станок	Деталь
	1	2	3	4
1	F	1	6	E+4
2	10	F+2	E	5
3	2	E+2	F+4	8
4	E	9	8	F

Необходимо построить график Ганта для исходного порядка запуска деталей в обработку, т.е. в последовательности 1-2-3-4-5. Затем следует составить пять решений задачи по обобщениям алгоритма Джонсона; для каждого решения построить график Ганта; для одного из решений сконцентрировать микропростои оборудования к концу производственного цикла; вычислить суммарные простои и длительность работы каждого станка в исходном графике Ганта и после концентрации микропростоев, сравнить полученные результаты и сделать выводы.

Задача завершается определением экономической эффективности наилучшего из решений по сравнению с исходным порядком запуска деталей. Экономическая эффективность определяется путем сравнения длительностей производственного цикла.

2.2.3. Задачи сетевого планирования комплекса работ

Многие организационные и технические мероприятия представляют собой сложную совокупность взаимосвязанных работ. Примерами таких мероприятий могут быть строительство и реконструкция цехов и любых других объектов, освоение новой техники и технологии, производство проектно-конструкторских работ и пр. При реализации таких проектов возникает ряд проблем: определение рациональных сроков начала и окончания той или иной работы, обеспечивающих выполнение всего мероприятия за минимальное время; распределение ресурсов между работами, минимизирующее суммарные затраты. В частности, отдельные работы могут оказаться “узким местом”, сдерживать проведение остальных мероприятий. Их следует выявить и выполнять заблаговременно или выделить на них дополнительные средства.

Сетевой график позволяет получить наглядное представление о порядке выполнения отдельных операций, а так же о взаимосвязях между ними. Он является моделью реализации мероприятия, на которой можно изучать последствия тех или иных решений с целью выбора наилучшей стратегии управления.

На сетевом графике каждая работа изображается стрелкой, а факт ее окончания, называемый событием, обозначается кружком (рис.2.2.18).

Рисунок 2.2.18 – Изображение работы и факта ее окончания на сетевом графике

Предположим теперь, что некоторая работа а₂ может начаться только после окончания работы а₁. В таком случае говорят, что работа а₂ опирается на работу а₁ (рис. 2.2.19)

Рисунок 2.2.19 – Работа а₂ опирается на работу а₁

Если же одна работа опирается на несколько других, то естественно, что она может начаться не ранее, чем закончится последняя из предшествующих. Логическая же связь со всеми остальными изображается в виде фиктивных работ, не требующих затрат времени и изображаемых пунктирными стрелками, идущими к началу данной работы. На рисунке 2.2.20 работа а₄ опирается на а₁, а₂ и а₃, но позже всех заканчивается а₂.

Рисунок 2.2.20 – Фрагмент сетевого графика с фиктивными работами

При построении сетевых графиков наиболее распространенными являются следующие ошибки:

1. Висячие вершины свидетельствуют о том, что соответствующие им работы в принципе не нужны. Соответствующий этому случаю фрагмент сетевого графика приведен на рис. 2.2.21.

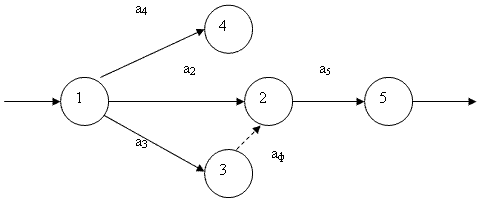Рисунок 2.2.21 – Фрагмент сетевого графика с “висячей вершиной”

1. Замкнутый цикл (зацикливание) свидетельствует о том, что комплекс работ в принципе не может быть выполнен. Соответствующий этому случаю фрагмент сетевого графика приведен на рис. 2.2.22.

Рисунок 2.2.22 – Фрагмент сетевого графика с “замкнутым циклом”