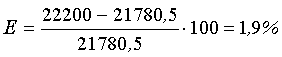8. Пример решения задачи оптимизации запасов ресурсов в условиях узкой специализации производства

Таблица 2.2.5

Исходные данные примера
Наименование ресурса	Запас ресурса	Цена ресурса за единицу, у.д.е.	Нормы расхода ресурса
			На 1 изделие вида А	На 1 изделие вида Б
Сырье С1	60	10	2	3
Сырье С2	60	20	3/5	2
Сырье С3	200	30	4	20

Прибыль от реализации единицы продукции вида А составляет 40 у.д.е., от реализации единицы продукции вида В – 30 у.д.е.

Математическая модель

2Х₁+3Х₂≤60; 3Х₁+2Х₂≤60; 4Х₁+20Х₂≤200; F=40Х₁+30Х₂→Мах.

По исходным данным, приведенным в табл. 2.2.5, определим рентабельность производства обоих видов продукции

R₁= 40/(2×10+3×20+4×30)×100=20%; R₂= 30/(3×10+2×20+20×30)×100=4,6%.

В результате принимается решение о производстве только первого вида продукции.

Суммарная стоимость используемых ресурсов:

D=60×10+60×20+200×30=7800 у.д.е.

С учетом (2.2.12) легко определяется X_r

и по (6.6) необходимые для этого запасы ресурсов в пределах имеющихся финансовых возможностей:

С₁=2×39=78; С₂=3×39=117; С₃=4×39=156.

При этом будет получена прибыль в размере

F=40×555=22200 у.д.е.

Таким образом, математическая модель задачи принимает вид:

2Х₁+3Х₂≤52; 3Х₁+2Х₂≤78; 4Х₁+20Х₂≤104; Х₁≥0; Х₂≥0; F=40Х₁+30Х₂→Мах.

Соответствующее этой модели графическое решение задачи приведено на рисунке 2.2.13.

Рисунок 2.2.13 – Графическое решение задачи

Оценка экономической эффективности решения задачи оптимизации запасов в условиях узкой специализации производства

Экономическая эффективность определяется по той же формуле, которая использовалась ранее:

Таким образом, экономическая эффективность решения этой задачи составила 2167 у.д.е. или 10%

Узкая специализация производства более эффективна и в данном случае позволяет увеличить прибыль на

9. Исходные данные задачи формирования производственной программы

Данная задача может быть решена в двух вариантах – вручную с помощью симплексного метода или на компьютере с помощью Excel. В первом случае трудоемкость задачи оказывается значительно выше, поэтому размерность задачи может быть уменьшена. В любом случае в результате решения задачи требуется определить количество продукции каждого вида, которое необходимо произвести при имеющихся ресурсах для получения максимальной прибыли. Затем необходимо корректировать запасы ресурсов с целью их полного использования и получения большей прибыли. При этом необходимо сделать не менее трех итераций при ручном счете.

Определить экономическую эффективность решения задачи оптимизации запасов ресурсов.

Определить рентабельность производства обоих видов ресурсов.

Решить задачу оптимизации запасов ресурсов в условиях узкой специализации производства.

Определить экономическую эффективность узкой специализации производства.