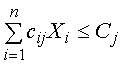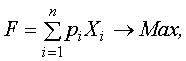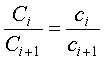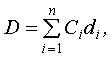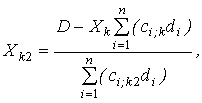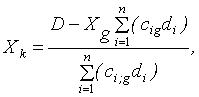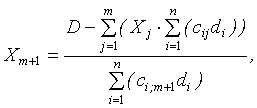7. Оптимизация запасов ресурсов в условиях узкой специализации работы предприятия

Задача оптимизации производственной программы предприятия в простейшем случае имеет вид:

	(2.2.4)
	(2.2.5)

где c_ij – нормы расхода j-го вида ресурсов на производство единицы i-го вида продукции;

C_j – запасы ресурсов j-го вида;

n – количество видов продукции;

m – количество видов ресурсов;

F – целевая функция (прибыль);

p_i – прибыль от реализации единицы i-го вида продукции.

Под ресурсами здесь следует понимать сырье, материалы, оборудование, трудовые ресурсы и пр.

Использование двойственного симплекс-метода показывает преимущества изменения одного ограничения по отношению с другими. В вышерассмотренной задаче двойственная оценка по второму ограничению оказалась выше, чем по третьему. Следовательно, увеличение запасов второго ресурса за счет реализации излишков первого позволит улучшить результаты решения в большей степени, чем увеличение запасов третьего ресурса.

Решение задачи оптимизации величины запасов ресурсов должно продолжаться путем реализации некоторой части ресурсов, приносящих меньшую прибыль с целью приобретения ресурсов более ценных с точки зрения целевой функции.

Увеличение запасов одного вида ресурсов за счет остальных в пределе приводит к выпуску только одного вида изделий, дающему наибольшую прибыль. Такая узкая специализация позволяет разработать самую простую типовую схему движения предметов труда, минимизировать внутрипроизводственные связи, уменьшить простои оборудование и пролеживание предметов труда, улучшить качество продукции и пр. В таком случае математическая модель задачи упрощается и принимает вид:

	(2.2.6)
	(2.2.7)

где r – номер наиболее рентабельной продукции;

X_r – количество наиболее рентабельной продукции;

Р_k – прибыль от реализации этой продукции.

Эта задача состоит не только в определении объема выпуска продукции X_r, но и в определении величины запасов необходимых для этого ресурсов C_i.

С учетом того, что все запасы должны быть израсходованы полностью, они должны быть пропорциональны их нормам расхода. При изменении запаса одного ресурса соответствующим образом должны быть изменены и запасы других ресурсов, потребляемых при производстве программирования видов продукции. Запасы ресурсов естественно должны быть пропорциональны нормам их расхода:

(2.2.8)

или с учетом (2.2.6)

(2.2.9)

Суммарная стоимость используемых ресурсов

(2.2.10)

где d_i – стоимость единицы ресурса i-го вида.

С учетом (2.2.6)

(2.2.11)

Отсюда легко определяется X_r

(2.2.12)

и по (2.2.6) необходимые для этого запасы ресурсов в пределах имеющихся финансовых возможностей.

В условиях острой конкурентной борьбы и с учетом возможного насыщения рынка такой подход далеко не всегда допустим, в связи с чем, в математическую модель приходится вводить соответствующие дополнительные ограничения вида:

	(2.2.13)
	(2.2.14)

где X_k;max – максимально возможный объем реализации k-го вида продукции;

X_g;min – минимально допустимый объем выпуска g-го вида продукции.

В первом случае X_k оказывается заданным. На производство этого вида продукции потребуются определенные деньги. Тогда задача сводится к определению количества второго по рентабельности вида продукции Х_k2 по формуле

(2.2.15)

где 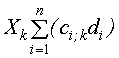– затраты на предельно допустимый объем выпуска наиболее рентабельной продукции.

Если же в силу некоторых обстоятельств выпуск некоторого вида продукции ограничен снизу, то

(2.2.16)

где – затраты на производство обязательной продукции.

Обобщая формулы (2.2.15) и (2.2.16) для любого числа ограничений сверху и снизу на выпуск продукции можно получить формулу, позволяющую определять объем наиболее рентабельной продукции из числа тех, на которые данные ограничения не распространяется

(2.2.17)

где m – количество видов продукции, на объем производства, которых наложены ограничения.

При этом запасы ресурсов должны вычисляться по формуле

(2.2.18)

Применение этих формул позволяет оптимизировать запасы ресурсов, свести к минимуму затраты, связанные с их хранением и обеспечивает выпуск наиболее рентабельной продукции при выполнении всех наложенных ограничений.