5. Анализ решения с помощью двойственного симплекс-метода

Симплексный метод позволяет получить оптимальное решение при имеющихся ресурсах, но не дает никаких рекомендаций об изменении запасов этих ресурсов с целью улучшения конечного результата. Эта проблема решается с помощью двойственного симплекс-метода.

Для перехода от прямой задачи к двойственной необходимо выполнить ряд операций. Матрица коэффициентов трансформируется. Правые части ограничений прямой задачи становятся коэффициентами целевой функции двойственной, а коэффициенты целевой функции прямой задачи становятся правыми частями ограничений двойственной. Знаки ограничений меняются на противоположные. Требование максимизации (минимизации) целевой функции меняется на требование ее минимизации (максимизации).

Таким образом, двойственная задача к той, что была рассмотрена в предыдущем разделе, будет иметь вид:

2У₁+3У₂+4У₃≥40; 3У₁+2У₂+20У₃≥30; F'=60У₁+60У₂+200У₃→Мin.

Решение двойственной задачи получается с учетом соответствия: прямым переменным прямой задачи соответствуют дополнительные переменные двойственной задачи, а дополнительным переменным соответствуют двойственные. В данном случае это соответствие выглядит следующим образом:

Решение двойственной задачи читается из последней симплексной таблицы следующим образом: двойственные оценки равны соответствующим оценкам в строке целевой функции. В данном случае У₁=0; У₂=1,3 и У₃=0,28. Это означает, что первый ресурс находится в избытке и увеличение его запасов не приведет к увеличению прибыли. Второй и третий ресурс в дефиците, и увеличение их запасов на единицу позволит увеличить выпуск продукции. Причем, увеличение запасов второго вида сырья предпочтительнее.

6. Аналитический метод решения с использованием программы Excel

В отличие от графического метода, аналитические методы (симплексные методы, метод Ньютона и др.) абсолютно точны. Кроме того, они дают возможность для точной количественной оценки излишков имеющихся ресурсов, дают еще и большие возможности для технико-экономического анализа полученного решения с целью выработки обоснованных рекомендаций по улучшению условий функционирования системы.

Рассмотрим решение задачи с помощью Excel на примере модели, построенной ранее (см. ф-лу (2.2.1)).

Исходные данные организуются так, как это показано на рисунке 2.2.11.

Рисунок 2.2.11 – Пример организации исходных данных задачи для решения ее в Excel

В ячейку Е7 записываем =СУММПРОИЗВ($B$5:$C$5;B7:C7). Здесь вычисляется значение целевой функции как сумма произведений фактического выпуска каждого вида продукции на прибыль от реализации ее единицы. Затем в ячейку Е10 записывается =СУММПРОИЗВ($B$5:$C$5;B10:C10). Здесь рассчитывается фактический расход каждого вида ресурсов, как сумма произведений норм расхода на фактический выпуск продукции каждого вида. Затем это копируется (растягивается) до ячейки Е15.

В ячейку I10 записываем =G10-E10 и копируем это до I15.

В ячейку J10 – =(G10-E10)/G10×100, до ячейки J15.

В ячейку С21 – =B21×G10, до С24;

В G21 – =F21×B21 до G24;

В К21 – =J21×B21 до К24;

В L10 – =G10-F21+J21.

После этого необходимо в меню выбрать «сервис» и «поиск решения». Затем необходимо заполнить появившуюся панель так, как это показано на рисунке 2.2.12, после чего дается команда «Выполнить» и «ОК».

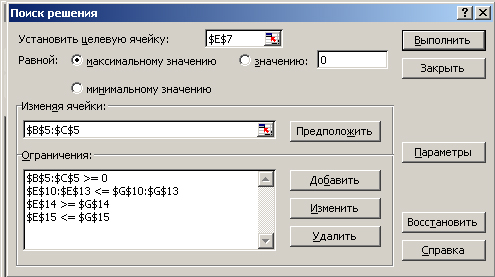Рисунок 2.2.12 – Ввод ограничений

В ячейках В5 и С5 появляется решение задачи – значения искомых переменных Х₁ и Х₂, а в Е7 – значение целевой функции. В ячейках I10-I15 – остатки ресурсов в единицах их измерения, а в J10-J15 – те же остатки в процентах от запасов.

После анализа остатков принимается решение о продаже наиболее избыточных из них. В данном примере продается 900 дней машинного времени, что записывается в ячейку F23. Точнее говоря, так как в данной задаче станки арендуются, то это означает сокращение срока аренды на 900 дней. При этом освобождается 18000 у.д.е. На эти деньги закупаем 600 единиц дефицитного сырья второго вида (18000/30=600).

В результате в ячейках L10-L13 появляются новые запасы, которые вручную записываются в ячейки G10-G15 для решения новой задачи с целью дальнейшей оптимизации запасов ресурсов.