Решение.

f(x) = 1,5x + 8sin(1,5x+2) в интервале [-5, 5]

Найдём производную данной функции:

= d(x)

Найдем корни производной:

1,5x + 12cos(1,5x + 2) = 0

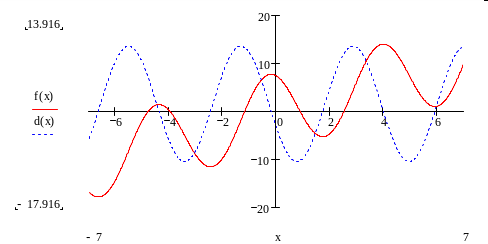
В данном интервале мы имеем 5 корней(экстремумов):

Х1 = -4,391; X2 = -2,464; X3 = -0,203; X4 = 1,725; X5 = 3,986

Составим таблицу знаков функции f(x):

x	-	-4,391	-2,464	-0,203	1,725	3,986	+
Sign f(x)	-	+	-	+	-	+	-

Из таблицы видно, что в данном интервале, функция имеет пять действительных корней:

С уточнением X1[-5; -4,391]; X2[-4, 391;-2,464]; X3[-2,464;-0,203]; X4[-0,203;1,725];

X5[1,725;3,986]

Уточним корень X2[-4,391;-2,464] для этого разделим участок пополам, и уточним, в каком из них находится корень. Зададимся длиной отрезка где лежит корень равной 0,1

Шаг1.

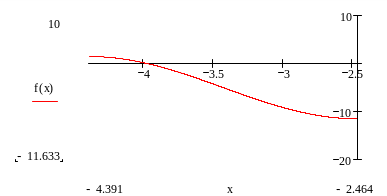
Как видно из графика корень лежит в промежутке

X2[-4,391;-3,4275] т.к. значение произведения функции на концах отрицательно

Шаг2. Делим промежуток [-4,391;-3,4275] пополам

Корень лежит в промежутке

X2[-4,391;-3,9] т.к. произведение значений функции на концах отрицательно

Шаг3. Делим промежуток X2[-4,391;-3,9] пополам и таким же образом определяем, что

корень лежит в промежутке [-4,146;-3,9]

Шаг4. Делим отрезок [-4,146;-3,9] пополам и по произведению значений функции на концах определяем, что корень лежит в промежутке [-4,02;-3,9]

Шаг5. Делим отрезок [-4,02;-3,9] пополам и по произведению значений функции на концах определяем, что корень лежит в промежутке [-4,02;-3,96]. На этом шаге останавливаемся, т.к. данный интервал соответствует заданной малости отрезка.

Задание 1.4. По заданной функции f(x) в заданных интервалах рассчитать интеграл методом Симпсона (интервал [a, b] разбить не менее чем на пять подынтервалов).

Решение.

f(x) = 1,5x + 8sin(1,5x + 2) в интервале [-5, 5]

Разобьем интервал на пять подынтервалов :

h = 2

Используя формулу для n участков найдем интеграл:

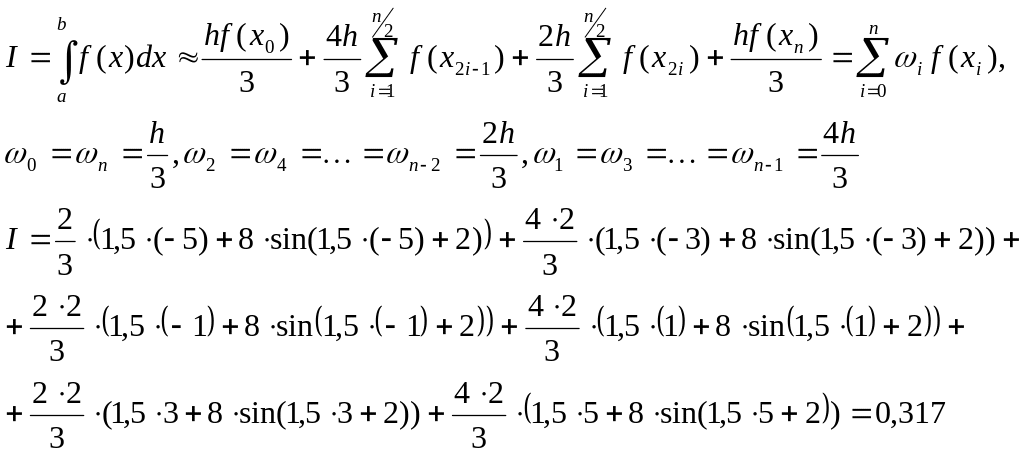
Задание 1.5. Задана система нелинейных уравнений: f1(x1, x2) = 0 и f2(x1, x2) = 0.

Решить её заданным в соответствии с номером варианта методом.

Решение.

sin(x1+1)-x2 = 1,2

2x1 + cosx2 = 2 Решаем методом итераций с погрешностью не хуже 0,001.

В качестве начальных условий принимаем х₁₀ = 0,45 х₂₀ = -0,16. преобразуем систему к виду, удобному для применения метода, путем выражения переменных из каждого уравнения :

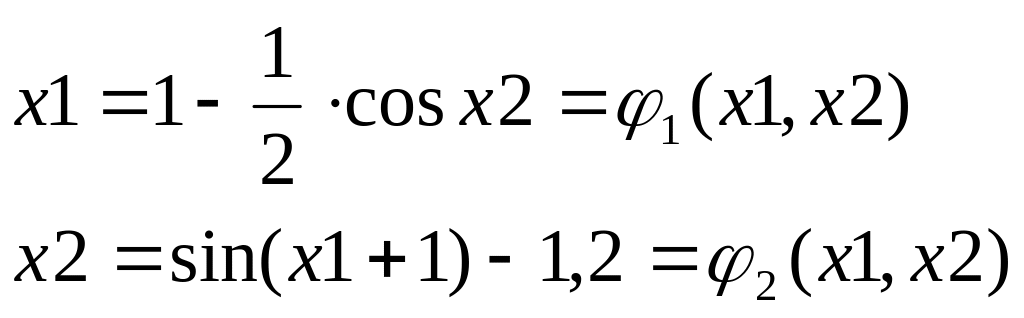
Проверим выполнение условий сходимости

Нетрудно заметить, что условия сходимости будут выполняться всегда:

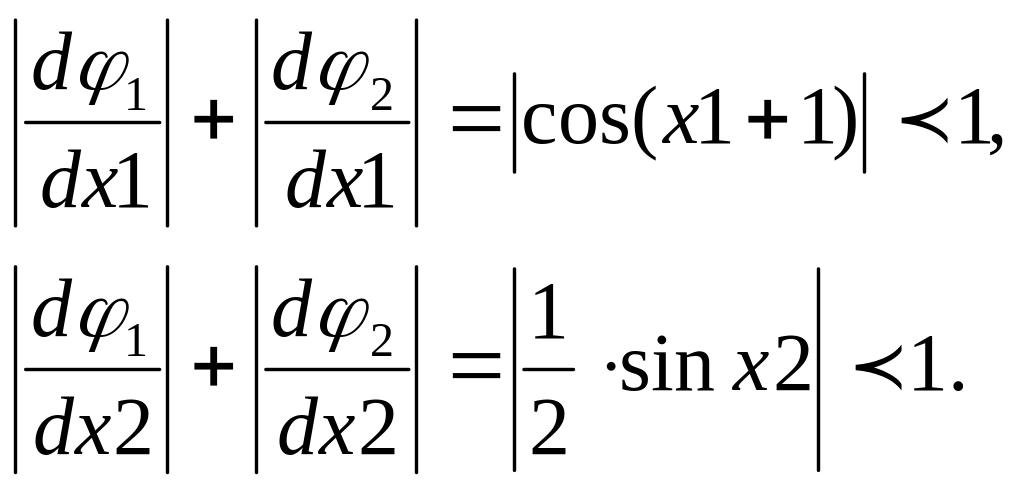
Шаг1

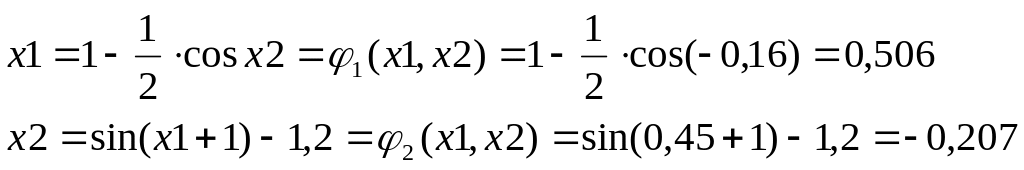
Шаг2

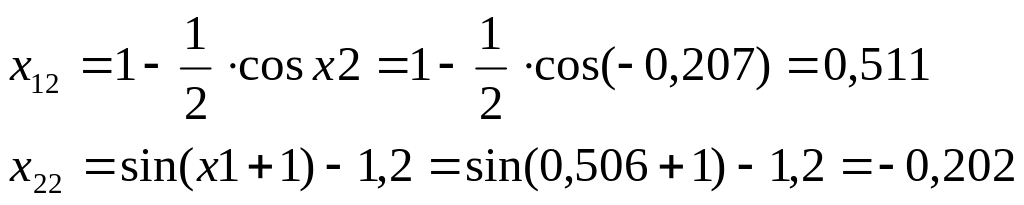
Шаг3

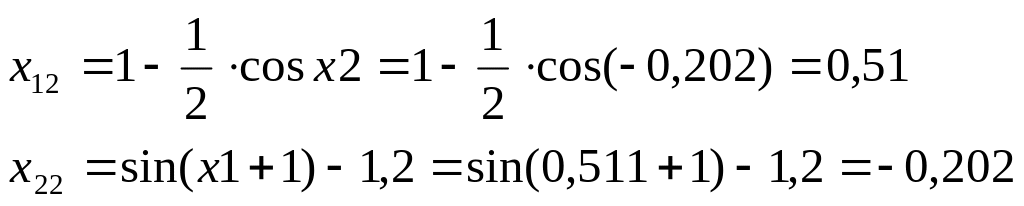
Ответ: x1 = 0,51 x2 = -0,202

Задание 1.6. Для заданного алгебраического уравнения Pn(x) = 0 найти общее число корней, предельное значение корня и выделить один действительный корень.

Решение.

Общее число корней n = 5 (степени полинома).

Количество действительных корней равно 3 или 1.

Количество действительных отрицательных корней равно 2 или 0.

Метод предельных значений: Чтобы найти область существования корней надо вычислить верхние границы положительных корней:

• для полинома Pn(x): ;

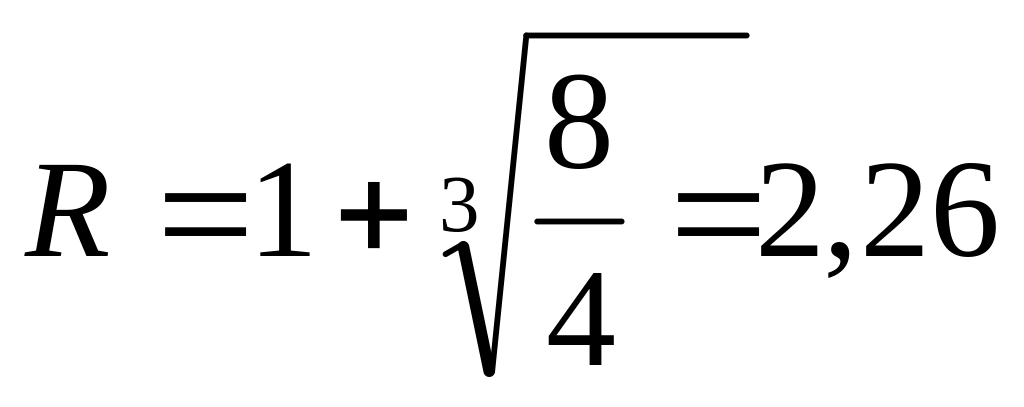• для полинома ;

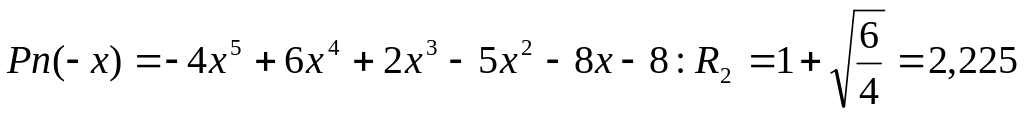• для полинома ;

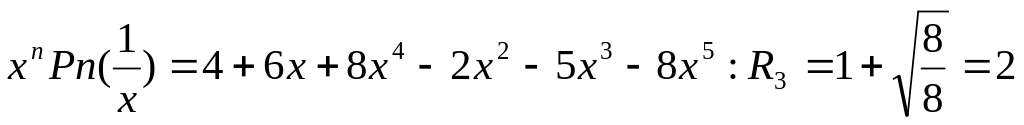• для полинома ;

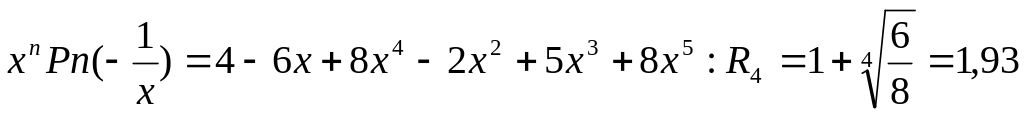Таким образом, если действительные корни существуют, то они лежат в интервалах [-2,225;-0,518] и [0,5; 2,26].

Выделим действительный корень :

где =0,5

Продолжая итерации можно прийти к выводу, что метод не сходится. Проверим условие сходимости:

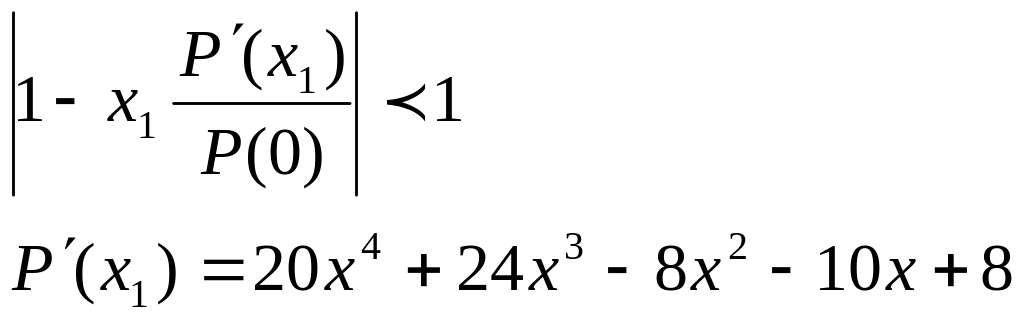
- корень уравнения;

Тогда

это условие нарушено. Метод не сходится.

Задание 1.7. Решить дифференциальное уравнение

при заданных начальных условиях в пределах [-5;5] с шагом не менее h = 1.