19. Расчет центрально-сжатых стержней на устойчивость с применением коэффициента продольного изгиба

Для сжатых стержней проводим две проверки:

на прочность:

где основное допускаемое напряжение на простое сжатие, коэффициент запаса, площадь поперечного сечения стержня с учетом местных ослаблений.

на устойчивость:

Допускаемое напряжение на устойчивость и допускаемое напряжение на прочность взаимно связаны. Составим отношение:

где коэффициент уменьшения основного допускаемого напряжения на простое сжатие (коэффициент продольного изгиба). Он всегда меньше единицы.

Коэффициент зависит от материала стержня и гибкости и принимается по таблицам. Условие устойчивости принимает вид:

При расчете стержня на устойчивость местные ослабления сечений не влияют на величину критической силы, поэтому в расчетные формулы вводится полная площадь поперечного сечения A_бpутто.

Различают два вида расчетов на устойчивость сжатых стержней: проверочный и проектировочный.

Проверочный расчет сжатых стержней.

Порядок расчета.

1. Зная размеры и форму поперечного сечения, определить площадь поперечного сечения А_бpутто и минимальный момент инерции J_min.

2. Вычислить минимальный радиус инерции и гибкость стержня по формулам:

3. По таблице найти значение коэффициента .

4. Проверить условие устойчивости

Проектировочный расчет сжатых стержней.

Условие устойчивости содержит две неизвестные величины, которые зависят одна от другой, – площадь поперечного сечения и коэффициент продольного изгиба . Задача при проектировочном расчете сжатых стержней решается методом последовательных приближений. В первом приближении принимают = 0,5, находят площадь сечения и устанавливают фактическое значение .

При большом различии между и выполняется второе приближение, т. е.

до тех пор пока разница в значениях между будет не более 5 %.

Далее окончательно определяются геометрические параметры поперечного сечения стержня.

20. Построение эпюр поперечных сил, изгибающих моментов и продольных сил для статически определимых плоских рам

Для статически определимой рамы (рис. 20, а) построить эпюры М, Q, N.

1. Мысленно разрезаем раму по шарниру F. Получим основную раму ADEFB и вспомогательную раму FGC.

2. Определим опорные реакции для вспомогательной рамы FGC (рис. 20, б).

3. Строим эпюры M, Q и N для вспомогательной рамы (рис. 20, в, г, д).

Эпюру Q строим по эпюре М, используя зависимость:

- участок, где сосредоточена распределенная нагрузка

- участок, где отсутствует распределенная нагрузка

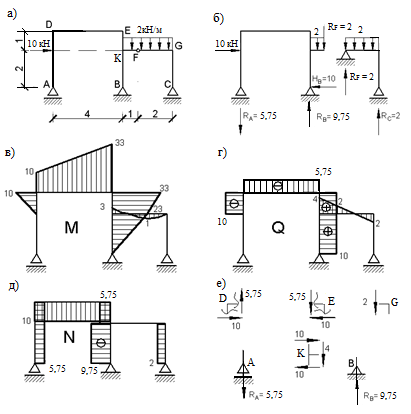
Рис. 20. Схема статически определимой плоской рамы

Эпюру N строим, вырезая узлы рамы и рассматривая их равновесие (рис. 20, е).

4. Определим опорные реакции для основной рамы ADEFB.

5. Строим эпюры M, Q и N для основной рамы ADEFB (рис. 20, в, г, д). Окончательные эпюры M, Q и N изображены на рис. 20, в, г, д.

21. Расчет плоской системы сходящихся сил графическим способом

Графическое определение усилий в элементах плоской системы связано с построением диаграммы Максвелла – Кремоны, что более наглядно можно представить при рассмотрении конкретного примера. Допустим, требуется определить графически усилия во всех стержнях фермы, изображенной на рис. 21. Вначале обычным способом определяем опорные реакции R_A и R_B.:

Затем нумеруем внешние и внутренние полигоны фермы. Полигоном называют область, ограниченную стержнями фермы или ее внешним контуром и нагрузками. В данном примере полигоны обозначены 1, 2, 3, … , 11, из них поля 1–5 – внешние, 6–11 – внутренние полигоны соответственно. Выбрав масштаб, откладываем все внешние силы в порядке обхода контура фермы по часовой стрелке. Номера точек начала и конца каждой силы соответствуют номерам полигонов, между которыми эта сила расположена.

Обходим ферму по внешнему контуру, за полигоном 1 следует полигон 2, откладываем на диаграмме точку 1, соответствующую началу силы F₁ и точку 2, соответствующую концу этой силы. Затем строим

Р ис. 21. Схема для определения усилий в стержнях фермы

с помощью диаграммы Максвелла – Кремоны

точку 3, соответствующую реакции R_B и так далее – точки 4, 5. Точки 1, 2, 3, 4, 5 должны лежать на одной прямой, но для наглядности они смещены по горизонтали.

Строим точки, соответствующие внутренним полигонам фермы, причем начинаем с полигона 6, так как он граничит с уже построенными ранее полигонами 1, 5. Из точки 5 проводим прямую, параллельную стержню AF, до пересечения с прямой, проведенной из точки 1, параллельной стержню АС. Получим точку 6. Затем можно построить точку 7, так полигон 7 граничит с двумя полигонами 1 и 6 (рис. 1.2.5, б), построенными на диаграмме. Из точки 6 проводим линию, параллельную стержню CF, а из точки 1 – прямую параллельно стержню CD. Их пересечение дает точку 7. Аналогично строится точка 8, после нее – точки 9,10. Последнюю точку 11 строим, используя полигоны 2, 10. В качестве проверки диаграммы проводим отрезок 3 – 11 и проверяем его параллельность стержню BH.

Для определения величины усилия в стержне фермы необходимо измерить длину отрезка диаграммы, соединяющего точки, соответствующие полигонам фермы, общей границей которых является данный стержень. Направление усилия, т. е. его знак получаем по номерам полей при обходе узла, в который входит данный стержень, по ходу часовой стрелки.

Так, например, усилие в стержне CD определяется величиной отрезка 1–7 на диаграмме. При обходе узла C по часовой стрелке получаем нумерацию 1–7, т. е. усилие N_CD направлено от точки 1 к точке 7 и является сжимающим.