40. Подпорные стенки. Общие понятия, расчетные предпосылки

Подпорные стенки устраивают в том случае, когда необходимо удержать массив грунта с откосом, крутизна которого превышает величину, определяемую углом внутреннего трения и силами сцепления. Типичным примером подпорной стенки является гранитная или бетонная набережная, удерживающая практически в вертикальном положении грунт на границе между сушей и водой.

Рассмотрим массивные подпорные стенки, которые характеризуются незначительным заглублением фундамента и большой толщиной. Такие стенки сопротивляются давлению грунта своей силой тяжести.

На рис. 40.1 изображена схема подпорной стенки, удерживающей клин земли, имеющий плоскую поверхность скольжения ВС (допущение Кулона). Устойчивость такой стенки должна быть проверена по трем показателям:

Рис. 40.1. Схема подпорной стенки

- не произойдет ли сдвиг стенки по плоскости основания АВ;

- не опрокинется ли стенка вокруг ребра A;

- не просядет ли стенка по основанию.

Размеры стенки и материал, из которого она сделана, считаются заданными. Все расчеты ведут для одного погонного метра длины стенки.

Вычисления начинают с определения основных сил действующих на стенку. Такими силами являются вес стенки G и активное давление грунта Е_а. Первая из них находится как объем стенки, умноженный на объемный вес материала, а для определения второй необходимо рассчитать и построить эпюру удельного давления грунта на стенку, для чего используется формула:

где удельное давление грунта в точке на глубине H_x; объемный вес грунта; внутренний угол трения.

Это выражение представляет собой уравнение прямой линии, поэтому эпюра удельных давлений будет иметь вид прямоугольного треугольника с максимумом удельного давления у подошвы стенки (рис. 40.1).

Равнодействующая активного давления грунта на подпорную стенку Е_а равна площади эпюры:

Равнодействующая будет горизонтальной и приложенной на одной трети высоты от низа подпорной стенки. В случае действия на поверхность грунта сплошной равномерно распределенной пригрузки q (кН/м²) определяем приведенную высоту слоя грунта h = q/γ, заменяющую ее действие, продолжаем заднюю грань стенки до пересечения с новой линией засыпки (рис. 40.2) и строим общую треугольную эпюру давлений. На подпорную стенку будет действовать только трапецеидальная заштрихованная часть эпюры давлений, тогда:

При вертикальной поверхности стенки давление Е_а будет действовать горизонтально в точке, соответствующей высоте расположения центра тяжести трапецеидальной эпюры давления (рис. 40.2). Однако подпорные стенки часто имеют заднюю грань наклонной, причем угол наклона β может быть положительным (рис. 40.2, б) или отрицательным (рис. 40.2, в).

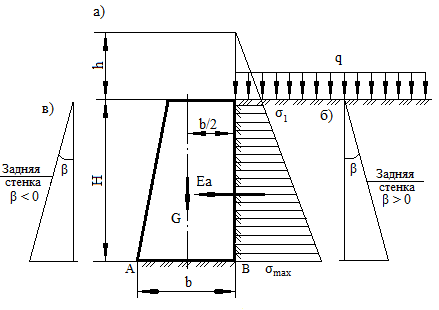
Рис. 40.2. Эпюра давления на подпорную стенку

при наличии пригрузки q

при β > 0

при β < 0

В случае загрузки поверхности грунта равномерно распределенной нагрузкой в последних формулах следует заменить множитель

Оценка устойчивости стенки. Определяем коэффициент устойчивости на сдвиг по формуле (рис. 40.1, 40.2):

где

Определяем коэффициент устойчивости на опрокидывание по формуле (относительно ребра А, рис. 40.1):

Определяем устойчивость стенки на просадку.

1. Линия действия силы G проходит через центр тяжести основания, тогда:

где

стенки прямоугольной формы; напряжения в точках А и B соответственно.

2. Линия действия силы G не проходит через центр тяжести основания, тогда:

с координата центра давления, представляющего расстояние от точки А (рис. 40.1) до того места, где равнодействующая сил G и Е_а пересекает линию основания стенки АВ.