21. Совместное действие изгиба и кручения.

Совместное действие изгиба и кручения. При совместном действии изгиба и кручения или кручения и растяжения(сжатия) простое суммирование невозможно ввиду разного характера напряжений (нормальные и касательные). Достоверные расчетные формулы для таких случаев могут быть получены на основании теорий прочности. Например, при совместном действии изгиба и кручения опасными являются точки, в которых нормальные напряжения от изгиба и касательные напряжения от кручения од­новременно имеют наибольшие значения. Подставляя значения главных напряжений из формулы , где α-коэффициент линейного температурного расширения стержня, выражения и , получаем условия прочности по теории наибольших касательных напряжений и энергетической теории прочности

;

где σ_эк — эквивалентное напряжение по теории наибольших касательных нап­ряжений; σ_эк — эквивалентное напряже­ние по энергетической теории прочности

22. Прочность при переменных нагрузках. Понятие об усталости материала.

Основные понятия. Наблюдениями установлено, что при действии в течение длительного времени нагрузки, периодичес­ки меняющейся от некоторого минимального до максимального значения, разрушение детали может произойти даже в том случае, когда наибольшие значения напряжения, возникающие при действии данной нагрузки, не превышают предела прочности σ_в и даже предел текучести σ_т. Нагрузка, изменяющаяся по определенному закону, называется циклической. Напряжения, вызываемые действием такой нагрузки, также называются циклическими. Совокупность последовательных значений переменных напряжений за один период процесса их из­менения называется циклом напряже­ний. Периодом цикла называется про­должительность одного цикла.

Явление разрушения материала де­тали под действием периодически меня­ющихся (циклических) напряжений но­сит название усталости материала.

Любой цикл м.б. охарактеризован средним напряжением: - амплитуда переменных напряжений. Рисунок симметричного напряж:

Важной характеристикой для этих графиков явл коэффициент асимметрии цикла:

(σ_max=σ_min) ( σ_min=0) σ_m – отсутствует

Явление разрушения материала де­тали под действием периодически меня­ющихся (циклических) напряжений но­сит название усталости материала.

Кривая усталости и понятие об усталости материала. Усталость – процесс переменного накопления повреждений под действием напряжений, приводящих к изменению свойств материалов и развитию трещин, а затем к последующему разрушению. Способность материала бесконечно долго выдерживать нагрузку не разрушаясь – выносливость. При симметричном цикле предел выносливости обозначается через σ_-1, при пульсирующей- σ₀, при ассиметричном – σ_r. N – число циклов напряжений. Nσ –базовое число циклов.

Смысл графика в том, что необходимо установить условия, когда стержень не разрушается. Расчет сопротивления усталости. Уточнение расчетов на сопротивление усталости отражает влияние разновидностей цикла. Напряжение статических и усталостных характеристик размеров, форм и состояния поверхности. Расчеты выполняются в форме проверки коэффициента запаса прочности

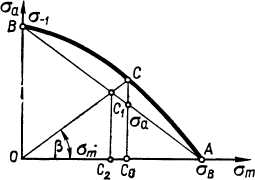
25. Диаграмма предельных напряжений

Предел выносливости при любом коэф­фициенте асимметрии цикла может быть найден с помощью диаграммы предель­ных напряжений — диаграммы устало­стной прочности Построение диаграммы основано на том, что любой цикл можно изобразить в виде суммы некоторого постоянного среднего напря­жения σ_т и симметричного цикла с амплитудным напряжением σ_а, причем σ_т и σ_а определяются по формулам и . При построении диаграммы по оси ординат откладывают амплитудное напряжение цикла σ_а, а по оси абс­цисс— среднее напряжение σ_m, величина которых определяется по значениям σ_max и σ_min, зафиксированном в соответствующих опытах над образцами. Т.о, предел выносливости при симметричном цикле изобразится точкой B, т.к для данного цикла ср напряжение σ_m =0. Предел прочности при статическом нагружении σ_B на диаграмме изобразится точкой А. Для некоторого произвольного цикла с амплитудным напряжением σ_А и сред­ним напряжением σ_m предел выносливос­ти на диаграмме изобразится точкой С. При этом Построение диаграммы усталостной прочности для данного материала диаграммой. При построении упрощенной диаграм­мы для данного материала достаточно знать значение предела выносливости при симметричном цикле _-1 и предела прочности при статическом нагружении . По этим значениям вместо экспери­ментальной кривой ВСА строят прямую ВА и довольствуются приближенными значениями пределов выносливости при различных характеристиках циклов. Для случая, показанного на диаграмме, приближенное значение предела вынос­ливости соответствует точке С₁ на упро­щенной диаграмме.С помощью диаграммы предельных напряжений значение предела выносливости можно определить, имея лишь значение коэффициента асимметрии цикла Как видно из диаграммы, Если задано значение коэффициента асимметрии цикла R_Oj то в соответствии с выражением определяется угол |3. Под этим углом из точки О проводит­ся Луч до пересечения с кривой ВС А (или с прямой ВС₁А —при использований упрощенной диаграммы. Предел выносливости при данном Rσ изобра­зится суммой отрезков ОС₀ + С₀С или ОС₂+С₂С₁