18. Расчеты на прочность и жесткость при изгибе.

Уравнение прочности. Из формулы видно, что нормальные напряжения по высоте сечения изменяются по линейному закону и, следовательно max , где - осевой момент сопротивления сечения, [м³]; для прямоугольного сечения высотой h и шириной b ; для круглой:

24. Изменение предела выносливости. Факторы, влияющие на предел выносливости.

1. Влияние концентрации напряжений - теоретич коэффициент напряжений. - эффективный коэффициент концентрации напряжен. Это отношение предела выносливости стандартного образца без дефекта к образцу с дефектом. α_σ – описывает поведение хрупких материалов, но при пост напряжениях k_σ - для пластичных материалов.

2. Влияние абсолютных размеров ε_σ – коэффициенты влияния размеров. . В зависимости от материала получатся различные кривые. 3-Малоуглеродистая сталь;2-образцы с умеренной концентрацией напряжений, сталь;1-образцы с закаленной концентр напряжений, сталь. Замечено, что пост растягивающее напряжение повышает предел выносливости

3. Учитывается сост пов-ти β_n . Чем выше предел прочности материала, тем существеннее влияние.

4. Учитывается температура В результате, если все сложить, ; -нормальный коэффициент запаса прочности.

Для симметричного знакопеременного цикла. Для несимметричного: ;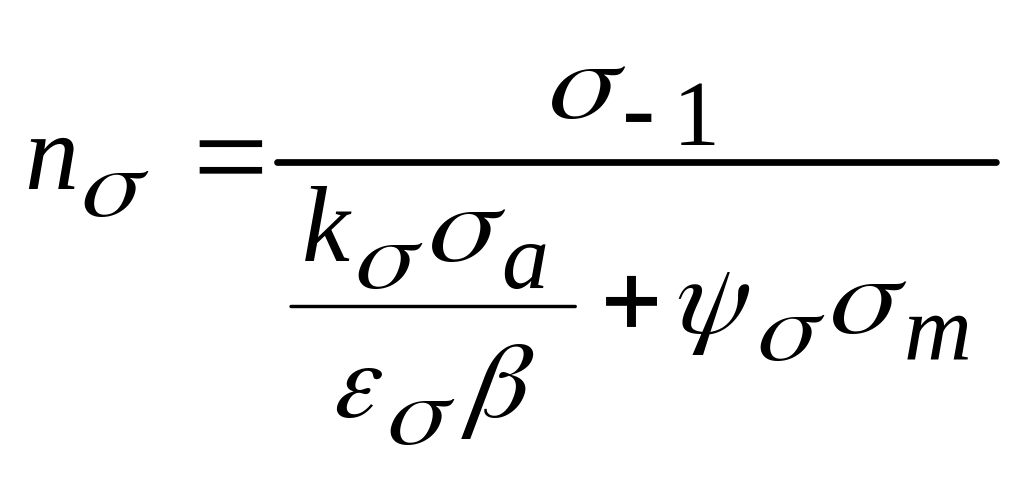

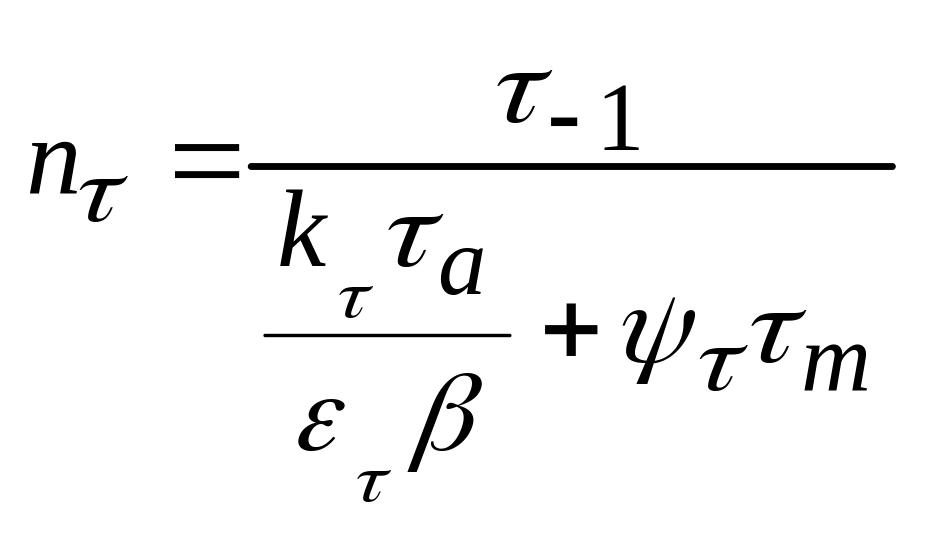
20 Гипотезы прочности. 3 и 4 гипотезы..

Теория наибольших касательных на­пряжений. По данной теории, предло­женной Кулоном, текучесть материала наступает тогда, когда наибольшее ка­рательное напряжение τ_mах до­стигает максимального значения, рав­ного наибольшему касательному напря­жению τ₄₅⁰_on при простом растяжении. Наибольшее касательное напряжение при плоском напряженном состоянии находится по выражению При простом растяжении Уравнение эквивалентности и условие прочности по данной теории можно за­писать окончательно в виде где [σ] — допускаемое напряжение при простом растяжении

Т еория наибольшей потенциальной энергии формоизменения (энергетиче­ская теория). Полную деформацию эле­мента можно условно представить со­стоящей из двух частей: деформации, приводящей к изменению объема тела без искажения его формы, и деформации, меняющей форму тела без изменения его объема. Первая часть деформации даже при очень высоких напряжениях не приводит к опасному состоянию, и поэтому величина потенциальной энергии, соот­ветствующая этой части деформации, также не может характеризовать степень опасности напряженного состояния. В связи с этим в качестве общего критерия прочности Губером было предложено принять удельную потенциальную энергию формоизменения:

;

Тогда условие прочности, можно записать в виде и_ф<и_оп, где опасное значение удельной потенциальной энергии деформации и_оп находится из опыта на растяжение. На основании изложенного уравнение прочности по энергетической теории с учетом формул и запишем в виде

При плоском напряженном состоянии (σ₃=0) Ф-ла

Эта теория прочности дает хорошие результаты при расчетах деталей пластических материалов, одинаково работающих на растяжение и сжатие