Метод гармонической линеаризации. (Метод гармонического баланса).

Метод позволяет нелинейные системы линейными уравнениями.

Метод основан на работах советских ученых Богомолова, Крылова, Попова.

Сущность метода гармонической линеаризации заключается в отыскании периодического решения на входе нелинейного элемента, разложении сигнала на выходе нелинейного элемента в ряд Фурье и его замены первой гармоникой.

1). Предположим, что нелинейная система представлена в виде 2-х частей: нелинейной и линейной.

2). На входе нелинейной части сигнал гармонический.

3). Нелинейная часть описывается уравнением вида:

(1)

(2)

2. частный случай уравнения (1) для гармонического сигнала.

Если на входе нелинейного звена действует гармонический сигнал , то сигнал на выходе нелинейного элемента может быть представлен в виде ряда Фурье.

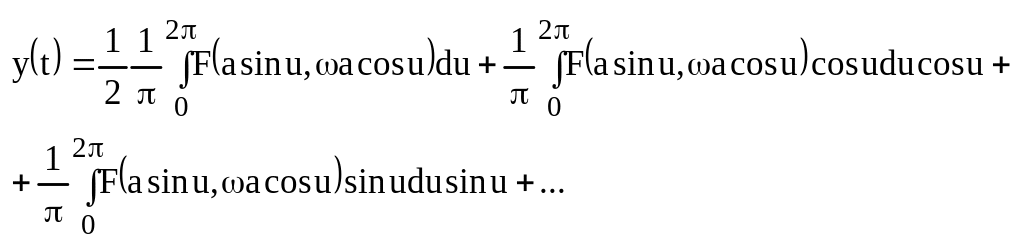(3)

Условимся:

1. функция F симметричная относительно начала координат, следовательно, отсутствует.

2. предположим, что высшими гармониками можно пренебречь. Основой такого предположения могут служить 2 гипотезы:

а) линейная часть системы представляет собой фильтр низких частот.

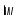
Идея гипотезы – частота 1-ой или основной гармоники меньше среды, а частота 2, 3, 4 и других высших гармоник больше среза.

б) линейная часть обладает резонансными свойствами, и как раз частоте 1-ой гармоники соответствует резонансная частота, которая вследствие этого превалирует в спектре выходного сигнала.

Для реальных объектов в промышленности наиболее справедлива 1-ая гипотеза, так как резонансные свойства там наблюдаются редко.

На этом основании мы отбросим высшие гармоники.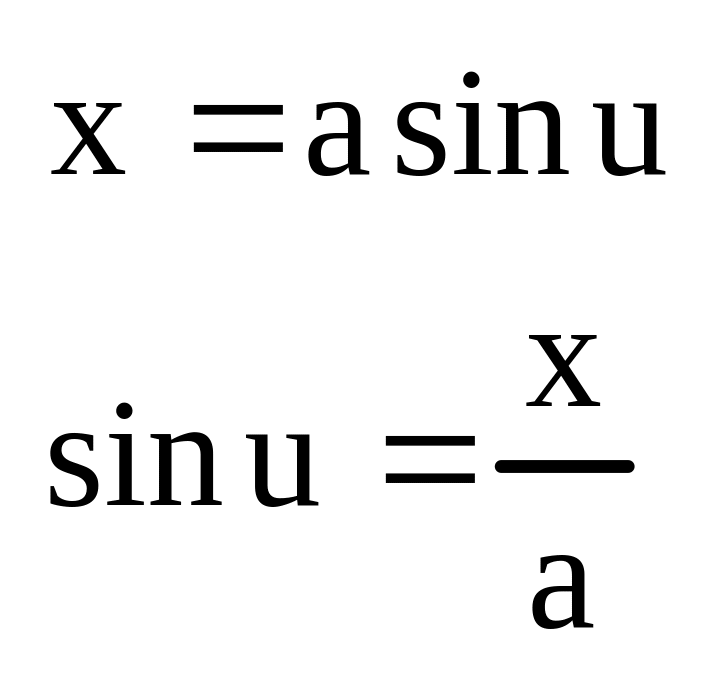

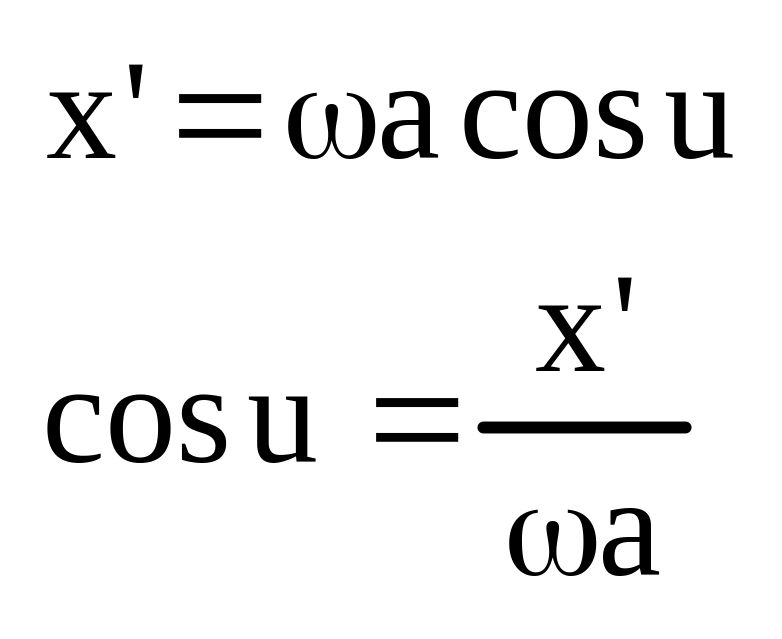
Уравнение гармонической линеаризации.

(4)

и - коэффициенты гармонической линеаризации.

(5)

(6)

Уравнение (4) – гармонически линеаризованное, однако оно сохраняет основные свойства нелинейного элемента, так как коэффициенты и зависят от и от . Это уравнение справедливо, когда на входе нелинейного элемента действует гармонический сигнал.

Примеры вычисления и для типовых нелинейных характеристик.

1. Релейная характеристика.

Запишем уравнение гармонической линеаризации для этого случая.

(7)

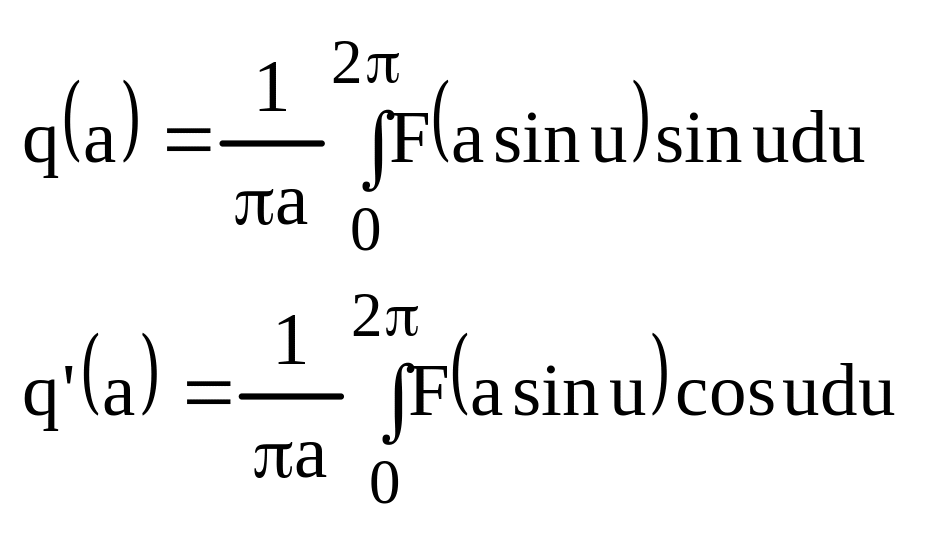
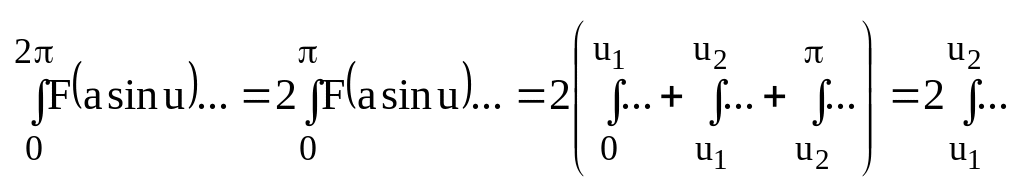
1. двухпозиционное реле с гистерезисом.

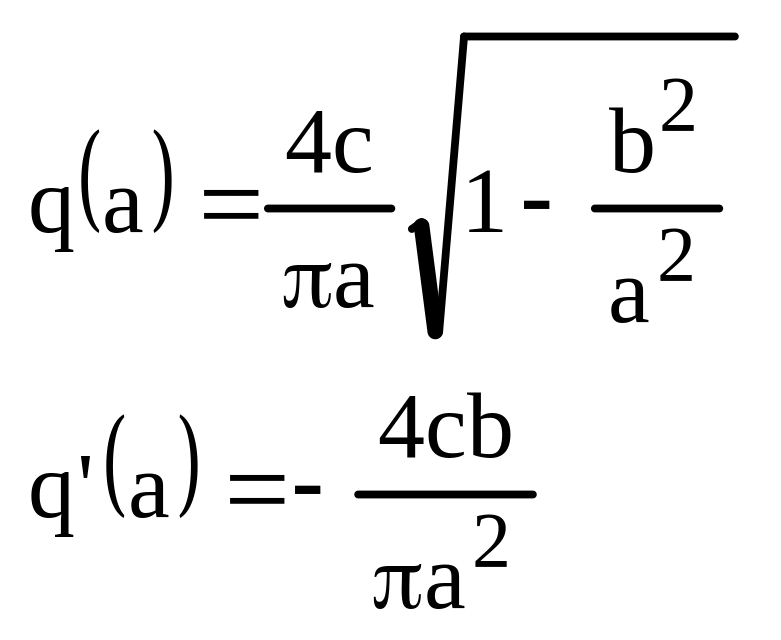
2. трехпозиционное реле с гистерезисом.

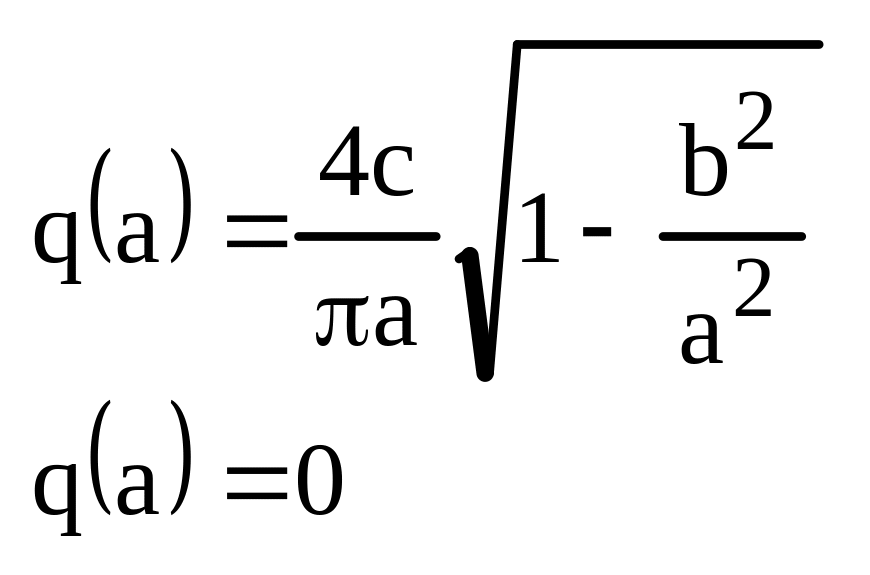
3. двухпозиционное реле без гистерезиса.

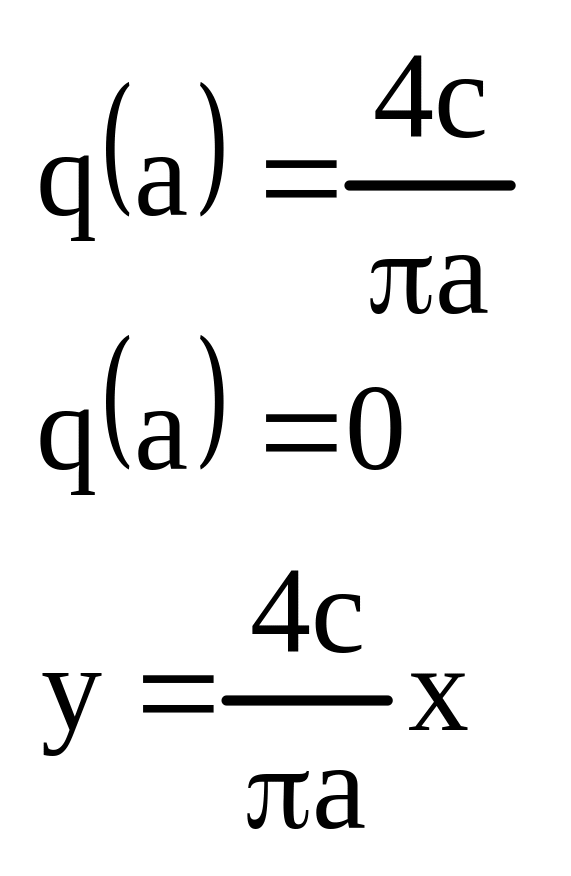
Устойчивость нелинейных систем.

Рассмотрим некоторую функцию

Функция называется знакоопределенной, если в некоторой окрестности начала координат она имеет постоянный знак и обращается в ноль только в начале координат.

Функция V называется знакопостоянной, если в некоторой окрестности начала координат она обращается в ноль не только в начале координат, но и в других точках.

Функция V называется знакопеременной, если она меняет знак в окрестности начала координат и равна 0 в начале координат.

Если функция V составлена относительно отклонений , входящих в в систему дифференциальных уравнений, описывающих нелинейную систему и если при всех функция V равна 0, то это функция Ляпунова.

Примеры:

1.

если и , то функция знакоопределенная, положительная.

если и , то функция знакоопределенная, отрицательная.

2.

, то знакопеременная.

3.

, то знакоположительная.

Введем понятие производной функции Ляпунова.

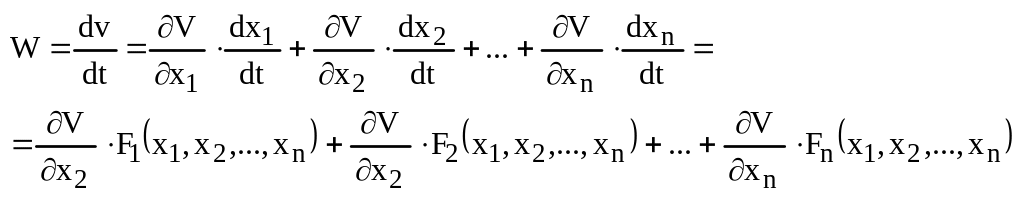
- эта функция так же как и функция Ляпунова V обращается в ноль при всех .

На основе этих функций формулируется теория устойчивости нелинейных систем.

Теорема: НЛС система устойчива, если можно подобрать такую знакоопределенную функцию V, по переменным входящим в систему (1), что ее производная W , знакоопределенной или знакопостоянной функцией, знак которой противоположен знаку V.

Если V принимает постоянное значение

Система будет устойчива, если скорость , т.е. .

Кроме того, скорость должна стремиться к 0 по мере движения к началу координат.

Если функция V является знакопостоянной, то точка М может застревать в некоторой точке, а система будет устойчива не асимптотически, относительно некоторой точки устойчивости.

Можно сформулировать обратную теорему:

Если W имеет тот же знак, что и V , то система будет неустойчива.

Недостатки теоремы Ляпунова:

1. на сегодняшний день нет общего метода для построения функции V.

2. возможность выбора функции V влияет на то, определим ли мы достаточное условие устойчивости и некоторую область устойчивости или не определим.

Частотный метод исследования устойчивости (метод Попова).

Метод более ограничен, но применяется чаще, так как проще.

Метод применим, если систему можно представить состоящей из нелинейной и линейной частей.

Нелинейная часть представлена в виде статической характеристики неоднозначной причем (1)

Условие (1) – это нежесткое условие.

Теорема устойчивости:

Для установления устойчивости нелинейной системы достаточно подобрать такое конечное действительное число h, что при всех положительных частотах выполняется неравенство

(2)

где - КЧХ линейной части .

то система устойчива асимптотически.

Если знаменатель передаточной функции имеет один нулевой корень, то накладывается требование

Если два нулевых полюса, тогда

Формулировка устойчивости простая, но ей неудобно пользоваться. Вводится видоизмененная частотная характеристика.

(3)

(4)

развернем выражение (2)

(5)

Рассмотрим прямую линию

она под наклоном h проходит через точку , система устойчива, если выполняется условие (5).

Для установления устойчивости НЛС достаточно подобрать такую прямую, проходящую через точку , что вся частотная характеристика будет находится правее этой прямой.

устойчивая система

Неустойчивая система, так как невозможно через точку провести некоторую кривую под наклоном h.

Форма нелинейности нас не интересует, нам необходима область на интервале .