Рекомендации к выполнению контрольной работы

Пример выполнения задания №1

Пусть производственная функция имеет вид Кобба-Дугласа. Для увеличения выпуска продукции на 3% необходимо увеличить основные фонды на 6% или численность работников на 9%. Один работник за отчетный период производит продукции на 100 000 руб., всего работников 1000 чел, основные фонды оценены в 10 млн.руб.

а) Составить производственную функцию.

б) Для полученной функции найти предельную производительность труда

и предельную фондоотдачу; среднюю производительность труда и

среднюю капиталоотдачу (фондоотдачу), а также капиталовооруженность

(фондовооруженность).

Решение:

а) Для получения параметров функции используется определение эластичности по факторам производства, процентное изменение аргумента делится на процентное изменение функции. Для степенных мультипликативных функций эластичность по факторам производства показывает, на сколько процентов изменится выпуск продукции, если фонды возрастут на 1 %, или число работников увеличится на 1 %. Следовательно, для переменной K степень 3:9 = 1/3, а для переменной L степень 6:9 = 2/3. Функция Кобба- Дугласа имеет вид . Найдем коэффициент A из остальных исходных данных, подставляя их в функцию Стоимость произведенной продукции (объем продукции в денежном выражении) получается умножением производительности ( в денежном выражении) одного работника на количество работников. Получаем уравнение . После вычислений на калькуляторе получим A= 4642. Таким образом, .

б) Для полученной функции найти предельную производительность труда и предельную фондоотдачу; величину средней производительности труда и средней капиталоотдачи (фондоотдачи), а также капиталовооруженность.

Частная производная по К имеет смысл предельной капиталоодачи (фондоодачи) и равна . Предельная производительность труда - частная производная по переменной L равна . Средняя производительность труда в денежном выражении за отчетный период Y/ L= 100000 руб. Средняя фондоотдача за отчетный период Y/K = = 10. Капиталовооруженность K/L= = 10000 руб. на одного чел.

Пример выполнения задания №2

В теории потребления предполагается, что потребитель всегда

стремиться максимизировать свою полезность и ограничением для него является величина дохода I, которую он может потратить на приобретение набора товаров. В задаче потребительского выбора необходимо найти такой набор , для которого

,

Поиск оптимального набора графически можно изобразить

как последовательный переход на кривые безразличия более высокого уровня полезности (рис. 1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством.

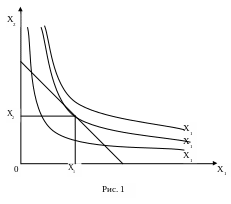
Для решения задачи используется метод Лагранжа. Составляется

функция Лагранжа:

,

где — множитель Лагранжа.

Для нахождения максимума функции приравняют к нулю все три частные производные этой функции, получается система уравнений:

Исключив из этих уравнений получают систему двух уравнений с

неизвестными :

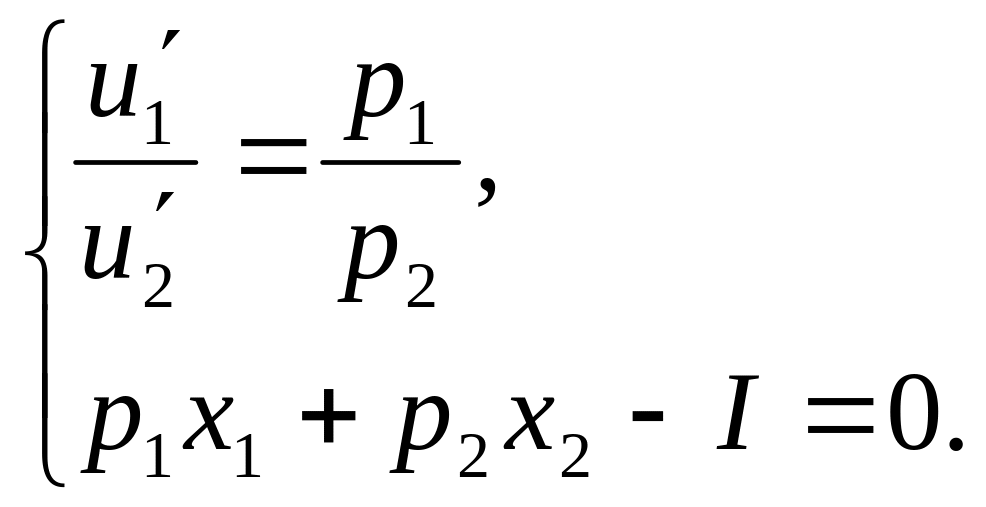
Из системы находится точка — решение задачи

потребительского выбора.

Пример. Функция полезности имеет вид Найти наилучший набор , если цена на товар равна д.е., на товар равна д.е., а доход составляет I = 400 д.е.

Решение. Дифференцируя функцию полезности, получим

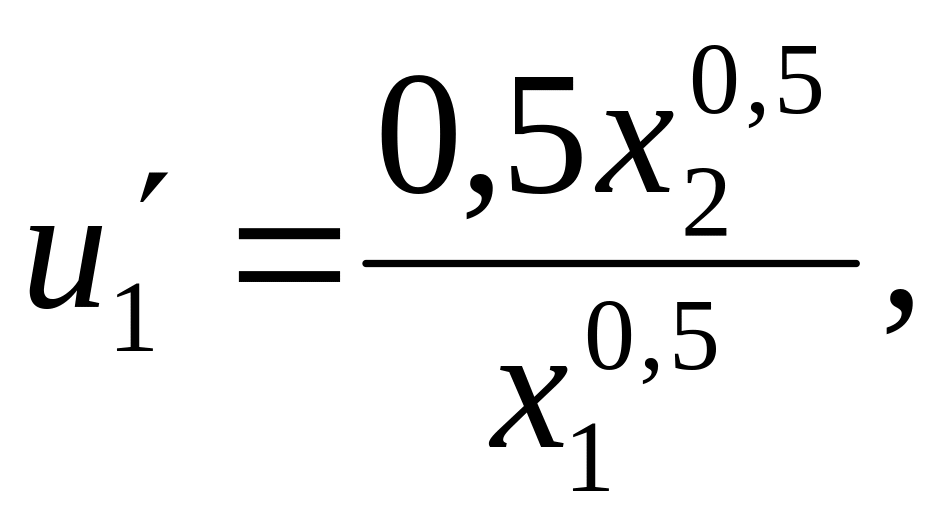
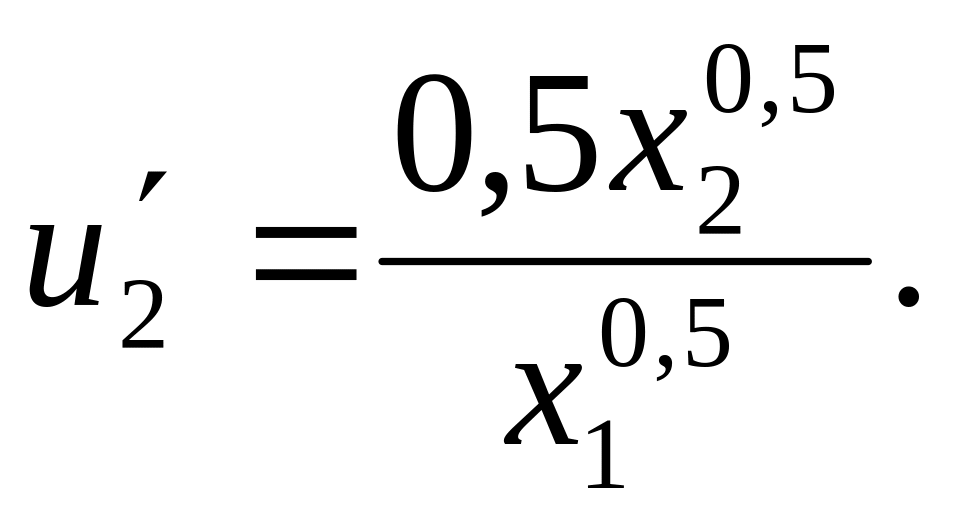
Подставляя выражения и , получим систему

То есть

Из первого уравнения следует, что затраты денежных средств на

оба товара должны быть одинаковыми, так как Из второго уравнения получаем, что функция спроса, задающая оптимальное количество товаров

Т.е.

Таким образом, расход на каждый товар составляет половину

дохода потребителя, а количество приобретенного товара равно затраченной на него сумме, поделенной на цену товара.

Пример решения задачи №3

Применение матриц в экономике. Пользуясь уравнением Леонтьева, X=AX+Y найти конечный продукт Y для каждой из трех отраслей, если известны объем совокупных продуктов каждой отрасли X и матрица коэффициентов прямых затрат A. Решить при ; .

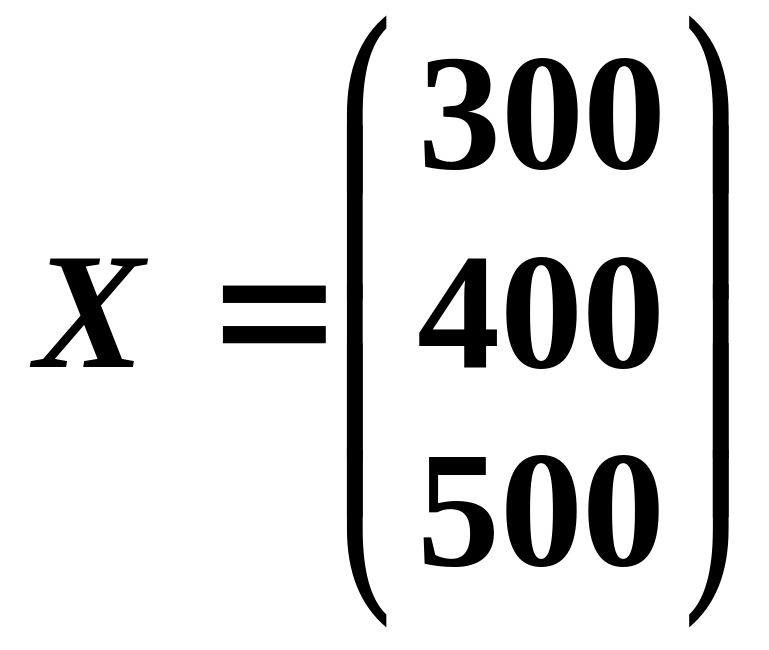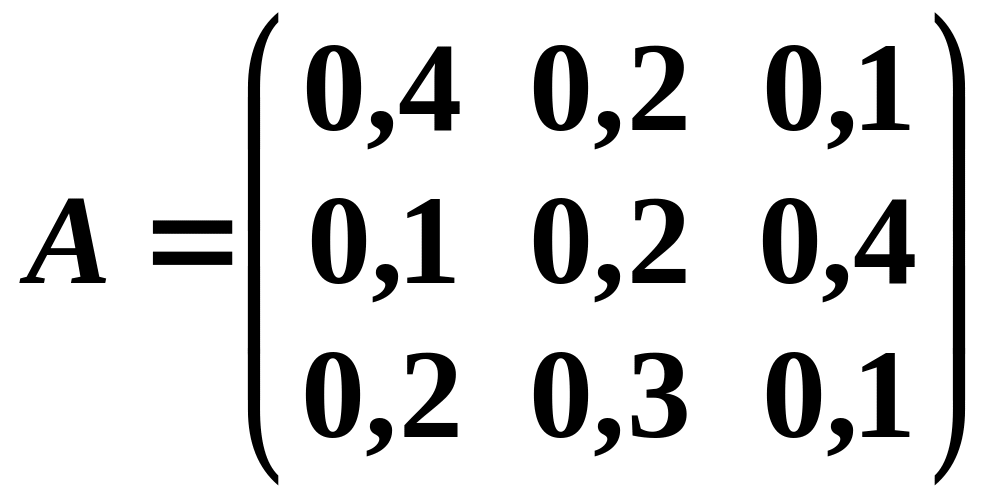Решение

Из уравнения Леонтьева X=AX+Y определяем Y по формуле: Y = X – AX .

= –  =

= – = .

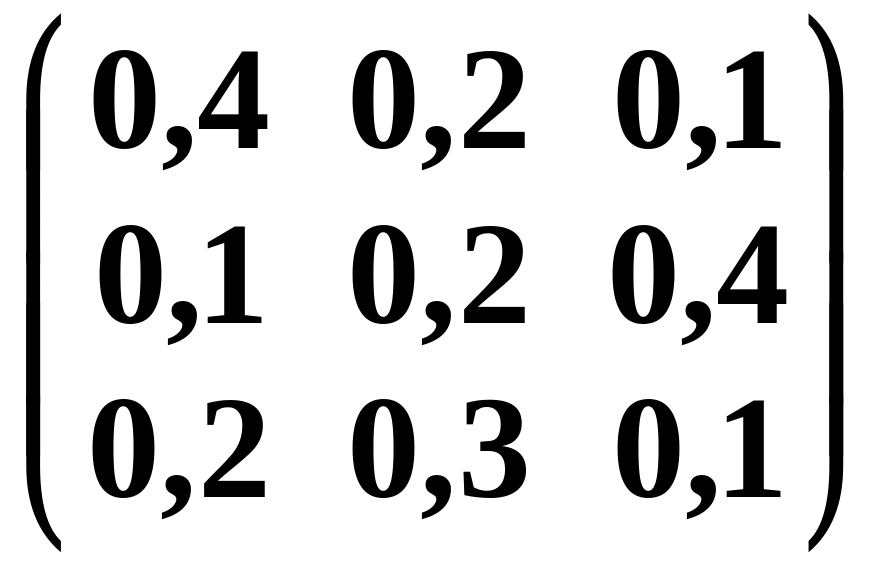
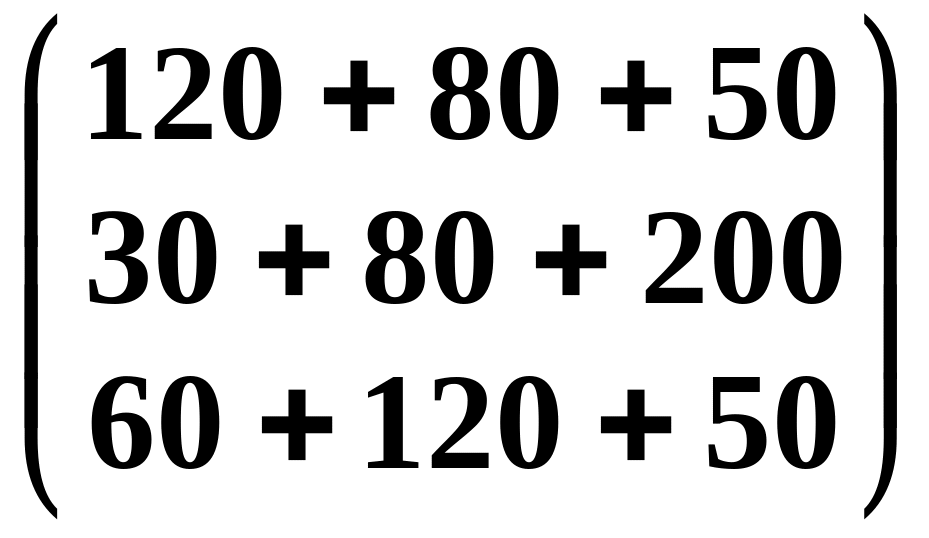Таким образом, y₁ = 50, y₂ = 90, y₃ = 270.

Пример выполнения теоретического задания №5