Метод z-буфера

Это один из простейших алгоритмов удаления невидимых поверхностей. Работает этот алгоритм в пространстве изображения. Идея Z-буфера является простым обобщением идеи о буфере кадра. Буфер кадра используется для запоминания атрибутов каждого пикселя в пространстве изображения, а Z-буфер предназначен для запоминания глубины (расстояния от картинной плоскости) каждого видимого пикселя в пространстве изображения. Поскольку достаточно распространенным является использование координатной плоскости в качестве картинной плоскости, то глубина равна координате точки, отсюда и название буфера. В процессе работы значение глубины каждого нового пикселя, который нужно занести в буфер кадра, сравнивается с глубиной того пикселя, который уже занесен в Z-буфер. Если это сравнение показывает, что новый пиксель расположен впереди пикселя, находящегося в буфере кадра, то новый пиксель заносится в этот буфер и, кроме того, производится корректировка Z-буфера новым значением глубины. Если же сравнение дает противоположный результат, то никаких действий не производится. По сути, алгоритм является поиском по и наибольшего значения функции .

Главное преимущество алгоритма - его простота. Кроме того, этот алгоритм решает задачу об удалении невидимых поверхностей и делает тривиальной визуализацию пересечений сложных поверхностей. Сцены могут быть любой сложности. Поскольку габариты пространства изображения фиксированы, оценка вычислительной трудоемкости алгоритма не более чем линейна. Поскольку элементы сцены или картинки можно заносить в буфер кадра или в Z-буфер в произвольном порядке, их не нужно предварительно сортировать по приоритету глубины. Поэтому экономится вычислительное время, затрачиваемое на сортировку по глубине.

Основной недостаток алгоритма - большой объем требуемой памяти. В последнее время в связи с быстрым ростом возможностей вычислительной техники этот недостаток становится менее существенным.

В целом алгоритм выглядит так:

0. Заполнить буфер кадра фоновым значением интенсивности или цвета.

1. Заполнить z-буфер минимальным значением z.

2. Преобразовать каждый многоугольник в растровую форму в произвольном порядке.

3. Для каждого Пиксель(x,y) в многоугольнике вычислить его глубину z(x,y).

4. Сравнить глубину z(x,y) со значением Zбуфер(x,y), хранящимся в z-буфере в этой же позиции.

5. Если z(x,y)>Z(x,y), то записать атрибут этого многоугольника (интенсивность, цвет и т.п.) в буфер кадра и заменить Zбуфер(x,y) на z(x,y).

6. В противном случае никаких действий не производить.

Методы приоритетов. Алгоритм художника.

В этих алгоритмах элементы сцены предварительно сортируются по приоритету глубины, основанному на расстоянии от точки наблюдения. Если такой список окончателен, то никакие два элемента не будут взаимно перекрывать друг друга. Тогда можно записать все элементы в буфер кадра поочередно, начиная с элемента, наиболее удаленного от точки наблюдения. Более близкие элементы к наблюдателю будут затирать информацию о более далеких элементах в буфере кадра. Поэтому задача об удалении невидимых поверхностей решается тривиально. Эффекты прозрачности можно включить в состав алгоритма путем не полной, а частичной корректировки содержимого буфера кадра с учетом атрибутов прозрачности элементов. Такой алгоритм называется алгоритмом художника.

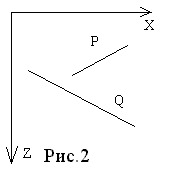
Необходимо сформировать предварительный список приоритетов по глубине, используя в качестве ключа сортировки значение Zmin для каждой грани. Первой в списке будет грань с минимальным значением Zmin. Эта грань лежит дальше всех от точки наблюдения, расположенной в бесконечности на оси +Z. Обозначим ее Р, а следующую в списке грань через Q (рис.1). Для каждой грани Р из списка надо проверить ее отношение с Q. Если ближайшая вершина Р (Pzmax) будет дальше от точки наблюдения, чем самая удаленная вершина Q (Qzmin), т.е. Qzmin>=Pzmax, то никакая часть Р не может закрывать Q. Следовательно, Р можно занести в буфер кадра.

Если Qzmin<Pzmax, то Р потенциально закрывает не только Q, но и любую другую грань типа Q из списка, для которого Qzmin<Pzmax. Тем самым образуется множество {Q}. Однако Р может фактически и не закрывать ни одну из этих граней, тогда Р заносится в буфер кадра.

Итак, перед выводом очередной грани Р следует убедиться, что никакая другая грань Q, которая стоит в списке позже, чем Р, и проекция которой на ось Оz пересекается с проекцией грани Р (если пересечения нет, то порядок вывода Р и Q определен однозначно), не может закрываться гранью Р. В этом случае грань Р действительно должна быть выведена раньше, чем грань Q.

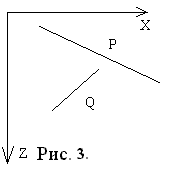
Приведем следующие тесты в порядке возрастания сложности:

1. Пересекаются ли проекции граней P и Q на ось Ох?

2. Пересекаются ли проекции граней P и Q на ось Оу?

Если хотя бы на один из этих двух тестов получен отрицательный ответ, то проекции граней Р и Q на картинную плоскость не пересекаются и, следовательно, порядок, в котором они выводятся не имеет значения. Поэтому будем считать, что грани упорядочены верно. Для проверки этих условий удобно использовать ограничивающие тела. В случае, когда оба теста дали утвердительный ответ, проводятся следующие тесты.

3. Находятся ли грань Р и наблюдатель по разные стороны от плоскости, проходящей через грань Q? (рис.2)

4. Находятся ли грань Q и наблюдатель по одну сторону от плоскости, проходящей через грань Р? (рис.3)

Если хотя бы на один из этих тестов получен утвердительный ответ, то считаем, что грани Р и Q упорядочены верно, и сравниваем Р со следующей гранью. Иначе необходимо поменять Р и Q местами, пометив позицию Q в списке и повторить тесты с новым списком.

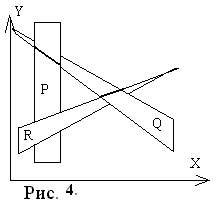
Если сделана попытка вновь переставить Q, значит обнаружена ситуация циклического экранирования (рис.4). В этом случае Р разрезается плоскостью несущей Q, исходная грань Р удаляется из списка, а ее части заносятся в список. Тесты повторяются для нового списка.