Лабораторна робота № 9 Процедурні типи

Мета роботи:

1. Засвоєння процедурних типів.

2. Отримання практичних навиків передачі процедур і функцій як параметрів при зверненні до інших процедур і функцій.

Теоретичні відомості для виконання лабораторної роботи

Обчислення інтегралів. Для обчислення інтегралів використовуються формули наближеного інтегрування.

1. Формула середніх прямокутників

,

де – кількість точок розбиття відрізка на рівні частини, – крок розбиття, , , .

2. Формула трапецій

,

де – кількість точок розбиття відрізка на рівні частини, – крок розбиття, , , , .

3. Формула Сімпсона (формула парабол)

,

де – кількість точок розбиття відрізка на рівні частини, – крок розбиття, , , , .

Обчислення інтегралів за згаданими формулами здійснюється з заданою точністю . Для досягнення заданої точності побудуємо процес обчислення значень інтеграла , , подвоюючи на кожному кроці кількість точок розбиття відрізка , тобто , де – початкова кількість точок розбиття, наприклад . Якщо виконується умова , то процес завершується, а вважається значенням інтеграла з точністю .

Розв’язування рівнянь. Розв’язування рівнянь виду

, (1)

складається з двох етапів: відокремлення коренів, тобто встановлення проміжків , , в кожному з яких міститься тільки один корінь; уточнення коренів, тобто їх обчислення з наперед заданою точністю . Для відокремлення коренів використовуються аналітичні або графічні методи. Для уточнення коренів використовуються ітераційні методи. Розглянемо деякі методи уточнення коренів.

1. Метод поділу проміжка навпіл. Якщо функція неперервна і набуває на кінцях проміжка значень різних знаків, тобто , то корінь рівняння (1) можна обчислити з наперед заданою точністю . Побудуємо обчислювальний процес. Обчислимо середину проміжка . Оскільки , то буде: , або , або . Якщо , то знайдено точне значення кореня і процес завершується. При корінь міститься на проміжку . Покладемо . При корінь міститься на проміжку .і Покладемо . Якщо довжина проміжка більша за , то знову обчислюється середина проміжка і т. д. Якщо довжина проміжка менша за , то процес обчислень завершується, а вважається наближенням кореня з точністю .

2. Метод ітерацій. Нехай на проміжку рівняння (1), де неперервна на функція, має єдиний корінь . Замінимо рівняння (1) еквівалентним йому рівнянням так, щоб , , а всі значення належали проміжку при .

Починаючи з деякого початкового наближення , знаходимо послідовні наближення за формулою

, . (2)

Обчислення завершуються при виконані умови

, (3)

при цьому вважається наближеним значенням кореня з заданою точністю .

Рівняння (1) завжди можна подати у вигляді так, щоб справджувалися вище наведені умови, наприклад,

, (4)

де – стала. При рівняння (4) і (1) еквівалентні. Сталу добирають так, щоб в околі кореня було тобто, щоб задовольнялися умови . Отже стала повинна мати той самий знак, що й , і задовольняти умову . Процес збігається тим швидше, чим ближче до нуля. Отже, слід добирати так, щоб добуток був якомога ближчим до для всіх .

3. Метод хорд (січних). Якщо функція двічі неперервно диференційовна на проміжку , похідні відмінні від нуля і зберігають знак на цьому проміжку, а , то за методом хорд наближене значення кореня знаходять як абсцису точки перетину хорди, що проходить через точки , з віссю .

Послідовні наближення кореня знаходять за формулою

, , (5)

де якщо , або якщо . Обчислення завершуються при виконанні умови

, (6)

де – задана точність, , При цьому вважається наближеним значенням кореня з заданою точністю .

4. Метод дотичних (Ньютона). Якщо функція задовольняє ті ж умови, що й у методі хорд, то за методом дотичних наближене значення кореня знаходять як абсцису точки перетину дотичної до кривої в одній із точок чи з віссю .

Послідовні наближення кореня знаходять за формулою

, , (7)

де якщо , або якщо . Обчислення завершуються при виконані умови

, (8)

де – задана точність, , , при цьому вважається наближеним значенням кореня з заданою точністю .

5. Комбінований метод. Якщо функція задовольняє ті ж умови, що й у методі хорд, і в методі дотичних, то для уточнення кореня зручно комбінувати метод хорд і метод дотичних. При цьому одержуються оцінки кореня зверху і знизу.

Послідовні наближення кореня знаходять за формулами

, (9)

, , (10)

де якщо , або якщо .

Обчислення завершуються при виконанні умови

, (11)

де – задана точність, при цьому вважається наближеним значенням кореня з заданою точністю .

Завдання:

Розробити програму обчислення таблиці значень інтеграла з заданою точністю для , що змінюється на інтервалі з кроком . Для обчислення значення інтеграла використати одну із формул наближеного інтегрування для завдань: 1-4 – прямокутників; 5-9 – трапецій; 10-14 – Сімпсона. У програмі використати підпрограму обчислення інтеграла за вказаною формулою, в яку передати підінтегральну функцію як параметр. Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення і відповідне йому значення інтеграла.

1. , , , .

2. , , , .

3. , , , .

4. , , , .

5. , , , .

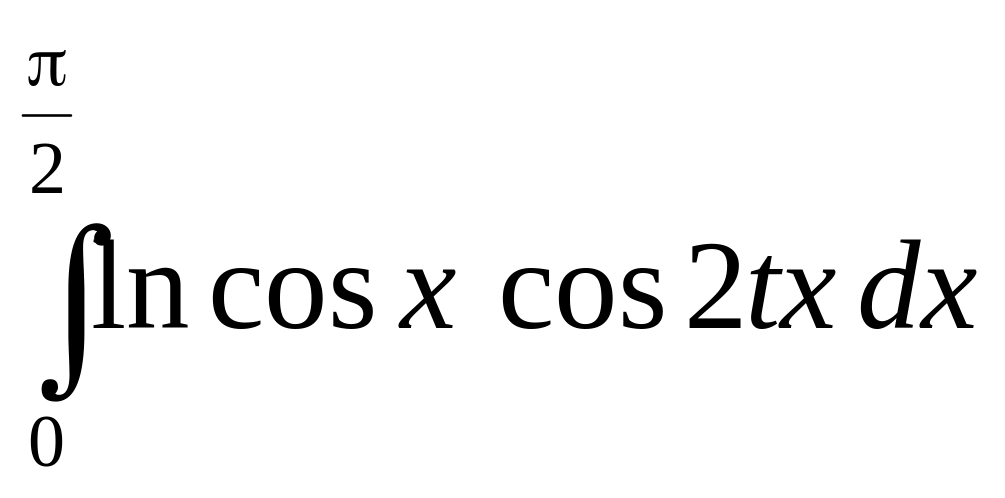6. , , , .

7. , , , .

8. , , , .

9. , , , .

10. , , , .

11. , , , .

12. , , , .

13. , , , .

14. , , , .

Розробити програму уточнення коренів рівняння на відрізку з точністю . Для уточнення коренів рівняння використати один із ітераційних методів для завдань: 15-18 – поділу відрізка навпіл; 19-21 – ітерацій; 22-24 – хорд; 25-27 – дотичних; 28-30 – комбінований. У програмі використати підпрограму уточнення коренів рівняння за вказаним методом, в яку передати як параметр функцію обчислення . Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення і відповідне йому значення кореня.

15. , .

16. , .

17. , .

18. , .

19. , .

20. , .

21. , .

22. , .

23. , .

24. , .

25. , .

26. , .

27. , .

28. , .

29. , .

30. , .