13. Розрахунок теоретичного та емпіричного значення відношення детермінації, його економічна інтерпретація. Обчислення кореляційного відношення.

Стандартна похибка моделі виражається в одиницях вимірювання результуючої змінної. Це робить неможливим порівняння 2-ох чи кількох КРМ на точність, якщо в них результуюча змінна вимірюється різними одиницями.

Для такого порівняння використовується безвимірна характеристика точності моделі і тісноти зв’язку – відношення детермінації.

Відношенням детермінації називають відношення поясненої дисперсії до всієї дисперсії результуючої змінної:

Із формули випливає, що відношення детермінації може приймати значення з інтервалу: .

Відношення детермінації є показником адекватності усіх кореляційно-регресійних моделей. А в нашому випадку (парна ЛКРМ) його називають коефіцієнтом детермінації

Для обчислення похибки моделі використовують пояснену дисперсію , то для обчислення відношення детермінації зручніше використовувати формулу:

Оскільки обсяг вибірки малий, то під час розрахунку використовуємо варіанси

R² =0,286

Отже, в середньому по Україні 28,6% зміни обсягу реалізованих послуг пояснюється зміною кількості малих підприємств.

Кореляційним відношенням називають арифметичне значення кореня квадратного з відношення детермінації:

Є показником сили зв’язку та адекватності моделі для всіх КРМ. Якщо КРМ є парною лінійною, то кореляційне відношення рівне абсолютному значенню коефіцієнта кореляції.

Оскільки R=0,4253, то зв'язок між факторною ознакою та результуючою змінною можна вважати слабким.

Загальну дисперсію результуючої змінної можна розкласти на суму поясненої та непоясненої дисперсії, як на основі ПЛКРМ так і на основі аналітичного групування. Формула декомпозиції загальної дисперсії змінної у має вигляд:

- кількість груп аналітичного групування;

- число одиниць сукупності в j-ій групі;

- фактичне значення результуючої змінної для і-тої одиниці сукупності j-тої групи;

- середнє значення результуючої змінної в j-ій групі.

Емпіричним відношенням детермінації називають величину:

Порівняння теоретичного відношення детермінації з емпіричним відношенням детермінації, дає змогу робити висновки про адекватність моделі.

=0,776

=100875922,9

У нашому випадку емпірична регресія пояснює 77,6%, а теоретична пряма –28,6% від загальної дисперсії результуючої змінної. Зв'язок між х і у доцільно описувати лінійною залежністю.

Етап 14: Обчислення вибіркових похибок параметрів регресії. Побудова довірчих інтервалів для істинних значень параметрів регресії, їх геометрична інтерпретація

Якщо при побудові ПЛКРМ методом найменших квадратів виконуються усі припущення класичного кореляційно-регресійного аналізу, то параметри b₀ i b₁ є величинами, розподіленими за нормальним законом.

Якщо замість дисперсії випадкових величин взяти її оцінку : , то формули для оцінки дисперсій b₀ i b₁:

Стандартною вибірковою похибкою вільного члена b₀ ПЛКРМ називають величину:

Гранична похибка вільного члена b₀ обчислюється за формулою:

За таблицями розподілу Стьюдента з рівнем значущості α = 0,05 значення імовірнісного коефіцієнта t_p = 2,069.

Геометрично довірчий інтервал для інтерпретується парою паралельних прямих, між початковими координатами яких з довірчою ймовірністю р знаходиться істинне значення цього параметра:

_{Довірчий інтервал для істинного} значення параметра :

Отже, з довірчою ймовірністю 95% можемо стверджувати, що істинне значення параметру β₀ належатиме довірчому інтервалу.

1840904,1	1845511,9	6692,19661	90333,83535
1827101	1831708,9	95874,51655	-26454,60561
1823889,6	1828497,4	116623,8706	-53626,86033
1826205,5	1830813,4	101660,3941	-34031,48433
1877557,8	1882165,7	-230129,7581	400463,3195
1824970,3	1829578,2	109640,9149	-44482,35153
1826205,5	1830813,4	101660,3941	-34031,48433
1842108,4	1846716,2	-1088,81117	100523,4309
1824476,3	1829084,1	112833,1232	-48662,69841
1823302,9	1827910,7	120414,618	-58591,02225
1835067,9	1839675,7	44400,15739	40953,48783
1845813,9	1850421,7	-25030,37357	131876,0325
1841243,7	1845851,6	4497,55339	93207,82383
1838619	1843226,8	21456,16009	70999,73103
1828521,5	1833129,3	86696,91763	-14436,10833
1826915,7	1831523,6	97071,59467	-28022,23569
1822870,5	1827478,4	123207,8003	-62248,82577
1840255,6	1844863,5	10881,97003	84847,13007
1824538	1829145,9	112434,0972	-48140,15505
1857548	1862155,9	-100845,3212	231159,2709
1829602,2	1834210,1	79713,96193	-5291,599526
1827101	1831708,9	95874,51655	-26454,60561
1823889,6	1828497,4	116623,8706	-53626,86033
1826205,5	1830813,4	101660,3941	-34031,48433
1877557,8	1879861,8	-230129,7581	400463,3195

Стандартна похибка оцінки коефіцієнта регресії b₁ обчислюється за формулою:

Гранична похибка оцінки коефіцієнта регресії b₀ обчислюється за формулою:

_{Довірчий інтервал для істинного} значення параметра :

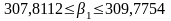
_{Отже, з довірчою ймовірністю 95% можемо стверджувати, що істинне значення параметру β1} належатиме довірчому інтервалу.

_{Цей довірчий інтервал геометрично інтерпретують парою прямих:}