Етап 17: Оцінення коефіцієнта кореляції.

Всі випадкові величини ми оцінювали до цього часу (випадкові відхилення, параметри b₀ , b₁) мали нормальний закон розподілу (або близький до нього), тому для їхньої оцінки можна було будувати симетричний довірчий інтервал, використовуючи таблиці нормального закону розподілу або розподілу Стьюдента:

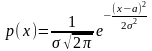
_{Коефіцієнт кореляції r не є нормально розподілена випадкова величина. Областю його допустимих значень є інтервал [-1;1], а нормального закону розподілу(-∞;+∞).}

_{Особливо сильно розподіл r відрізняється від нормального при тісному зв’язку між змінними, тобто коли r за абсолютною величиною близький до одиниці.}

_{Щоб мати змогу оцінити r в таких випадках Фішер запропонував спочатку перейти від випадкової змінної r до випадкової змінної z:}

Він показав, що випадкова величина z розподілена за нормальним законом розподілу з математичним сподіванням:

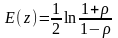, де ρ – істинне значення r для генеральної сукупності;

та дисперсією:

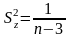
Тоді стандартна вибіркова похибка випадкової величини z:

Гранична вибіркова похибка z при заданому значенні довірчої ймовірності р:

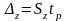
Припустимо, що ζ – невідоме значення випадкової величини z, яке відповідає коефіцієнту кореляції ρ, тоді довірчий інтервал для значення ζ має вигляд:

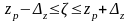, де z_p – значення випадкової величини z, яке згідно з відповідає вибірковому коефіцієнту кореляції r.

Введемо позначення:

z₁=z_r-Δ_z z₂=z_r+Δ_z

Тоді .

Здійснивши обернене перетворення від змінної z до змінної r за формулою:

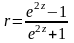
отримаємо довірчий інтервал для істинного значення коефіцієнта кореляції ρ генеральної сукупності 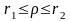, де

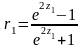
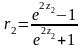
Якщо значення r близьке до 0, тобто зв'язок між змінними слабкий, то розподіл випадкової величини r надлижається до нормального, особливо при великих обсягах вибірки. В таких випадках стандартну похибку коефіцієнта кореляції визначають за формулою: 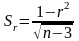. Далі оцінка істинного значення коефіцієнта кореляції проходить за звичною схемою.

_{1. Переходимо від випадкової змінної r до випадкової змінної z:}

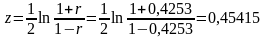
2. Стандартна вибіркова похибка випадкової величини z:

3. Гранична вибіркова похибка z при заданому значенні довірчої ймовірності р=0,95, рівні значущості α=1-р=0,05:

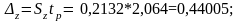
4. Визначаємо довірчий інтервал невідомого значення ζ випадкової величини z , яке відповідає істинному значенню коефіцієнта кореляції ρ :

0,0141≤ ζ ≤ 0,8942;

5. Здійснюємо обернене перетворення від змінної z до змінної r, отримаємо довірчий інтервал для істинного значення коефіцієнта кореляції:

r₁= 0,65489;

r₂= 0,81254;

0, 65489 ≤ ρ ≤ 0,81254;

З ймовірністю 0,95 можна очікувати, що істинне значення коефіцієнта кореляції генеральної сукупності ρ набуватиме значення не менші від 0,65489 і не більші від 0,81254.

Етап 18:Перевірка статистичної значущості параметрів зв’язку між змінними.

Гіпотези – судження про генеральну сукупність. Такі судження стосуються виду невідомого розподілу або параметрів відомого розподілу. Сформульовану гіпотезу будемо називати нульовою (основною) і позначимо 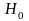. Протилежну називають конкуруючою (альтернативною) і позначають 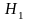. Обґрунтувати або спростувати гіпотези про генеральну сукупність на основі даних вибірки з цієї сукупності називається статистичним доведенням. Висновки отримані статистичним доведенням здійснюється за такою схемою:

1. на основі даних вибірки формуємо нульову гіпотезу , яку хочемо обґрунтувати або спростувати;

2. відповідно до нульової гіпотези вибираємо критерій (статистику);

Критерій – спеціальна підібрана випадкова величина, точний або наближений розподіл, якої відомий і яка служить для перевірки нульової гіпотези.

Статистика часто має розподіл Гауса (нормальний) або близький до нього, а саме розподіл Стьюдента, розподіл Фішера- Стьюдента, Хі -квадрат.

3. вибираємо рівень значущості - ймовірність відкинути згідно вибраного критерію істинну гіпотезу (має бути малою);

4. знаходимо, як правило, з таблиць критичні значення статистики k_кр= k_α, які відповідають рівню значущості α;

5. на основі даних вибірки обчислюємо емпіричне значення статистики;

6. робимо висновок про правомірність нульової гіпотези

Перевірка статистичної значущості коефіцієнта регресії.

Стосовно коефіцієнта регресії сформулюємо таку нульову гіпотезу: коефіцієнт регресії β₁ генеральної сукупності рівний нулю.

_{Статистика для перевірки цієї гіпотези має вигляд:}

_{Критичні значення tкр= tα цієї статистики призаданому рівні значущості α знаходять за таблицями розподілу Стьюдента з (n-2) ступенями вільності.}

Якщо t_ем > t_кр, то нульову гіпотезу відхиляють і з довірчою ймовірністю р=1-α вважають, що коефіцієнт кореляції ρ генеральної сукупності відмінний від 0.

Якщо t_ем ≤ t_кр, то нульову гіпотезу ймовірністю р=1-α немає підстав відхиляти нульову гіпотезу.

Шукаємо t_кр в таблиці t-розподілу Стьюдента:

t_кр =2,807 при =0,01

Перевірка статистичної значущості коефіцієнта кореляції.

Висуваємо нульову гіпотезу, що коефіцієнт кореляції між величиною валового регіонального продукту та кількістю зайнятих по регіонах України рівний 0. Отже, для перевірки Н₀ використовуємо емпіричне відношення статистики:

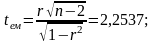
За таблицями Стьюдента при заданому рівні значущості _{α=0,01 та кількістю ступенів вільності 25-2=23 знаходимо критичне значення статистики}

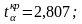
Оскільки емпіричне значення статистики більше за табличне, то з ймовірністю р=0,99 вважаємо, що коефіцієнт кореляції генеральної сукупності відмінний від 0, тобто кореляційна залежність обсягу побутових послуг від кількості підприємств побутового обслуговування по регіонах України є статистично значущою.

Перевірка статистичної значущості коефіцієнта регресії.

_{Висуваємо нульову гіпотезу, що коефіцієнт регресії β1} генеральної сукупності рівний нулю. Отже, для перевірки Н₀ використовуємо емпіричне відношення статистики,використовуючи t-статистику Стьюдента:

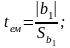
За таблицями Стюдента при заданому рівні значущості 0,01 та кількості ступенів вільності 23 знаходимо критичне значення статистики :

t_ем < t_кр,

_{То нульову гіпотезу приймаэмо, і з ймовірністю р=0,99 вважаємо, що коефіцієнт регресії не відмінний від нуля, тобто залежність} обсягу побутових послуг від кількості підприємств побутового обслуговування по регіонах України не є статистично значущою.