Последовательность линейных фильтров
Последовательность фильтров можно заменить суммарным фильтром, который будет их сверткой.
Таким образом, результирующий фильтр будет иметь размер (2w-1)(2w-1)
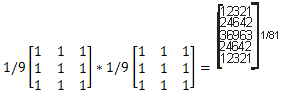
Статистические фильтры
В результате их применения на выходе получим новое изображения, которое характеризует локальные статистические свойства данных. Хотя СТ оценки рассчитываются в небольшой окрестности каждого пикселя и обладают низкой значимостью из за небольшого объема выборки, но не смотря на это они могут быть полезны для решения задач по подавлению шума, выделение границ, выделение текстуры изображении. в результате применения фильтра из изображения будут исключены те пиксели которые не починяются типичной статистике в текущем окне. Медианный фильтр наиболее полезный, позволяет удалить отдельные пиксели, которые соответствуют небольшому участку.
Морфологический фильтр
В результате применения фильтров макс и мин значений результирующего изображения представляет карту локальных мин и максимумов исходного снимка. При использовании фильтров минимальных значений для бинарных изображений получается тот же результат что и при использовании дилатационного фильтра. Действие фильтра в максимальных значениях при обработке бинарных значений эквивалентно эррозионноному фильтру.
Области применения этих фильтров.
Пространственная сегментация и подавление шума.
При морфологической обработке окно операции называют структурирующим элементом. Такой элемент может использоваться для сопоставления с эталонами или изменениями определенных форм.
Градиентные фильтры
В частности они подчеркивают границы. Градиент может, вычислен путем фильтрации изображения в двух перпендикулярных направлениях, потом их сложением для расчета градиента.
Величина градиента определяется длинной составного вектора, а направление - углом между вектором и осью абсцисс. Наиболее распространенный фильтр Робертса, Собела и Превита.
Фильтр Робертса
Рачитываем градиент фи = arctan(gy/gx) |g|= корень из gx2+gy2
Фильтр Собела
Фильтр Превита
Выделение границ - задача бинарной классификации, которую можно решить с помощью пороговых значений модуля градиента. При этом слишком низкий порог может привести к выделению большого числа пикселей и появлению широких нечетких границ, а слишком высокий порог может привести к разбиению границ на несколько
Преобразования Фурье
Основа теории Фурье – представление одномерных и многомерных сигналов в виде линейных комбинаций базисных синусоидальных функций.
Фурье анализ
Первая компонента имеет нулевую частоту (нулевая гармоника). Т.к. представляет собой среднее значение сигнала. Компонента с наименьшей нулевой частотой имеет тот же период, что и прямоугольный сигнал и называется основной гармоникой. Третья гармоника имеет частоту в 3 раза больше, чем в основной гармонике. 5-ая гармоника в 5 раз больше.
Относительные веса этих компонент при их суммировании для синтеза исходного прямоугольного сигнала равны соответственно 1, 1/3, 1/5. По мере добавления новых компонент с больше частотой сумма их всё точнее будет описывать прямоугольный сигнал. Полная сумма всех компонент называется рядом Фурье прямоугольного периодического сигнала. Т.к. изображение у нас дискретное, то ряд Фурье представляет собой конечную сумму синусов и косинусов. Так же как и в 1-мерном случае ряда Фурье, исходное изображение воспроизводится полностью только при использовании всех членов разложения. С увеличением слагаемых повышается точность аппроксимации исходного изображения. Причём каждую такую сумму можно рассматривать как низкочастотную компоненту, а карту невязок – как высокочастотную.