
- •Задание на курсовую работу:
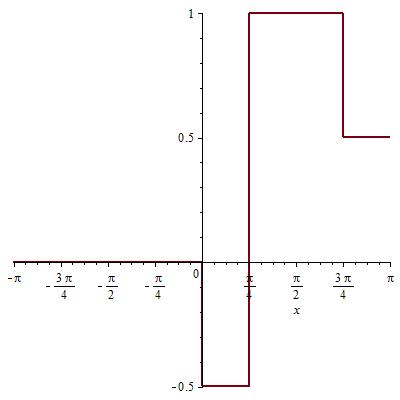
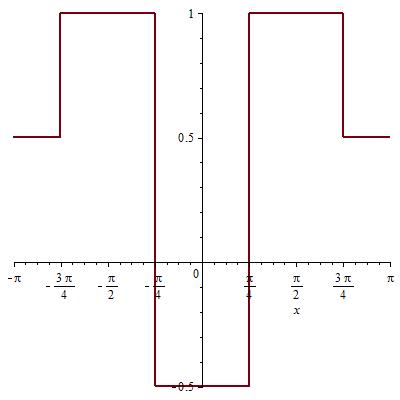
- •График:
- •1.Введение
- •2.Теоретическая часть.
- •2.1 Гармонический анализ
- •2.2 Ортогональные системы функций
- •2.3 Тригонометрический ряд Фурье
- •2.4 Теорема Дирихле о достаточных условиях разложения функции в ряд Фурье
- •2.5 Разложение различных видов функций в ряд Фурье
- •3.1 Задание функций аналитически.
- •3.2 Проверка всех необходимых условий
- •3.3 Расчёты
- •4. Заключение.
- •5. Используемая литература.
3.1 Задание функций аналитически.
Исходная функция:
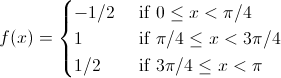
Произвольно продолженная:
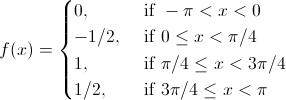
Продолженная чётным способом:

Продолженная нечётным способом:
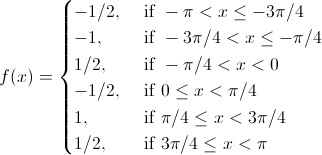
3.2 Проверка всех необходимых условий
Проверка достаточных условий разложения функции в ряд Фурье a) Функция f(x) является кусочно-непрерывной, то есть имеет конечное число точек разрыва 1-го рода, которые разбивают функцию на непрерывные отрезки.
б) Функция f(x) есть кусочно-монотонная функция, то есть монотонная на кусочках.
Следовательно,
соответствующий функции f(x)
ряд Фурье сходится на промежутке [-π,π],
при этом в точках непрерывности сумма
ряда совпадает с самой функцией, а в
каждой точке разрыва сумма ряда равна![]()
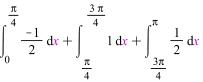 =
=
![]() < ∞
< ∞
3.3 Расчёты
Ряд Фурье общего вида
Найдём коэффициенты разложения:
>
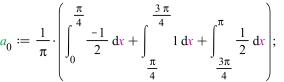
![]()
>
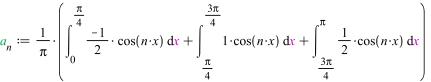
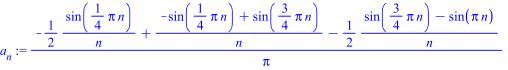
>

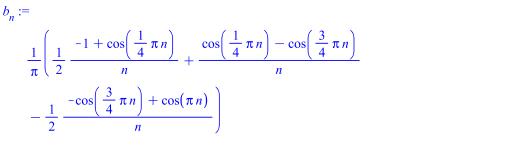
Ряд Фурье:
>
![]()
Графики сумм гармоник с наложением исходной функции:
0ая и 1ая гармоника: Сумма 0,1,2 гармоник:
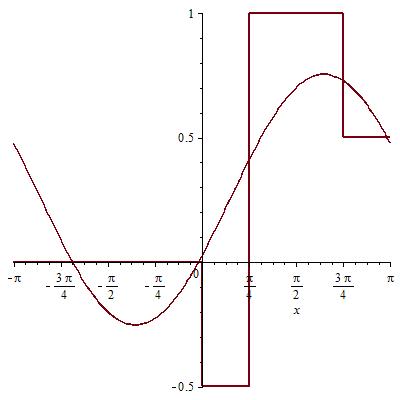
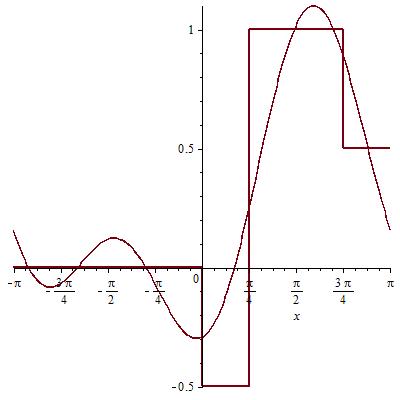
Сумма 0,1,2,3 гармоник: Сумма 300 гармоник:

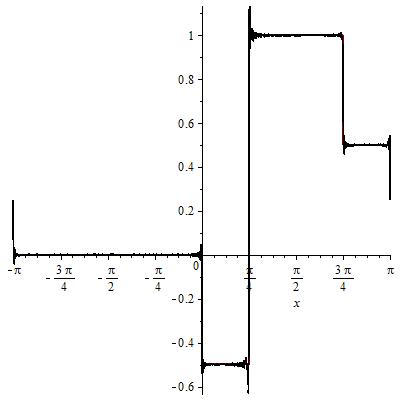
График амплитудных спектров
![]()
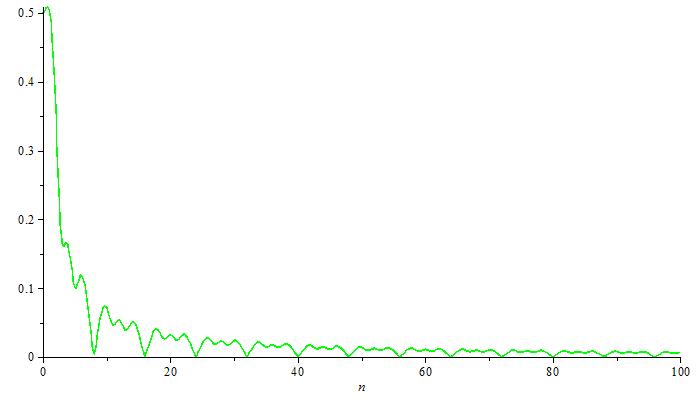
Средние квадратические ошибки.
При:
n=1 eps= 0.2528396300;
n=2 eps= 0.1802576880;
n=3 eps= 0.1538366535;
n=15 eps= 0.07472719333.
Интеграл Фурье
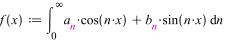
Ряд Фурье по синусам.
Найдём коэффициент разложения:
>
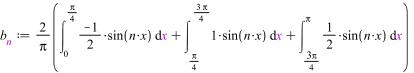
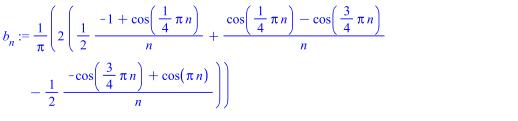
Ряд Фурье:

Графики сумм гармоник с наложением исходной функции:
0ая и 1ая гармоника: Сумма 0,1,2 гармоник:

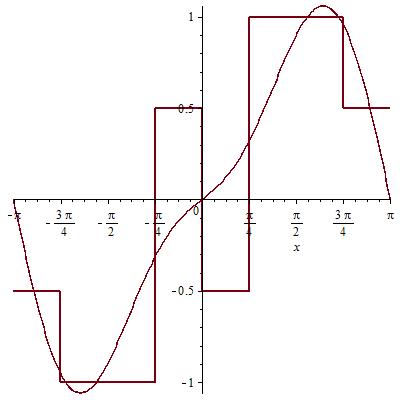
Сумма 0,1,2,3 гармоник: Сумма 300 гармоник:
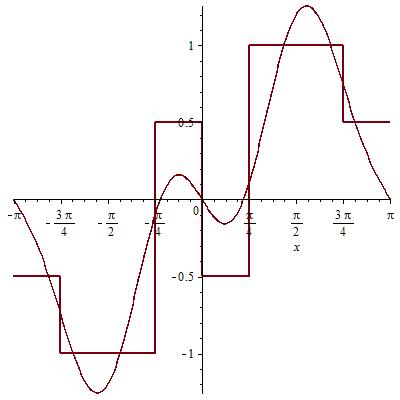
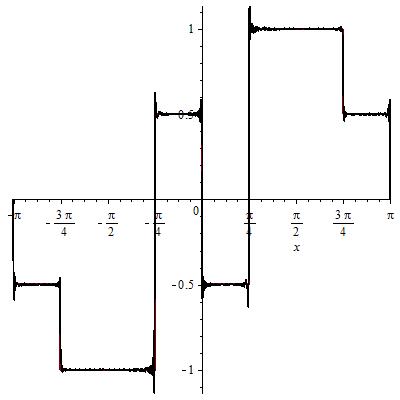
График амплитудных спектров

Средние квадратические ошибки.
При:
n=1 eps= 0.2951519488;
n=2 eps= 0.1503715533;
n=3 eps= 0.1379423802;
n=15 eps= 0.07083387859.
Интеграл Фурье.

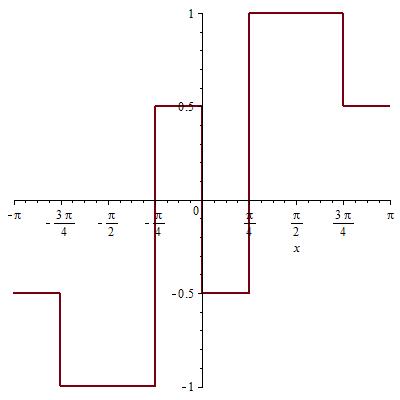
Ряд Фурье по косинусам.
Рассчитаем коэффициенты разложения:
>
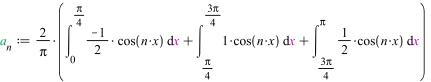

>
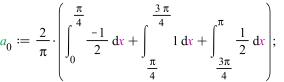
![]()
Ряд Фурье:
>
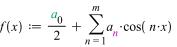
Графики сумм гармоник с наложением исходной функции:
0ая и 1ая гармоника: Сумма 0,1,2 гармоник:
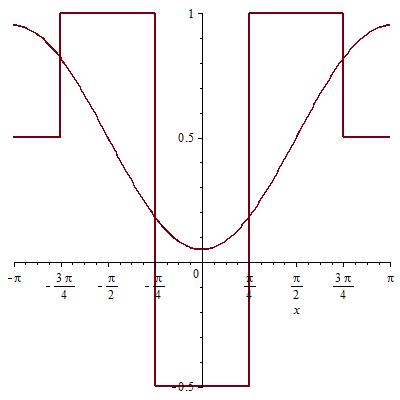
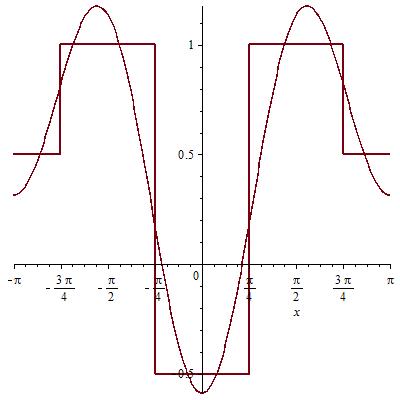
Сумма 0,1,2,3 гармоник: Сумма 300 гармоник:
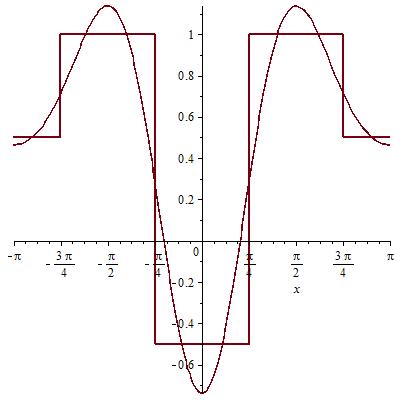
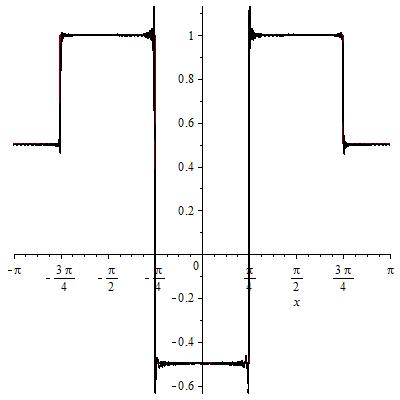
График амплитудных спектров
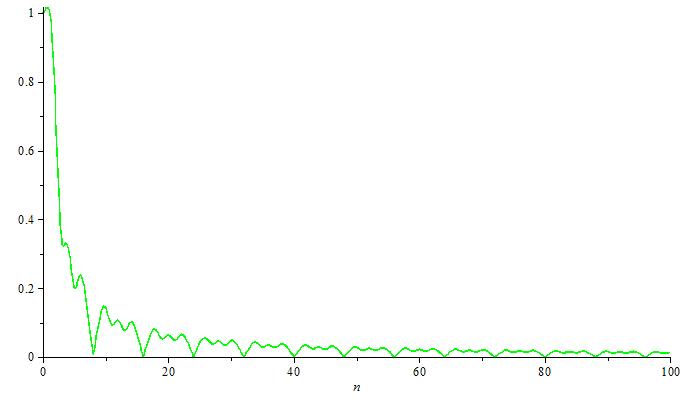
Средние квадратические ошибки.
При:
n=1 eps= 0.3271223635;
n=2 eps= 0.2061697649;
n=3 eps= 0.1972877800;
n=15 eps= 0. 0.1578347435.
Интеграл Фурье.
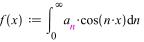
4. Заключение.
В данной работе был проведен гармонический анализ функции. Были проверены достаточные условия разложения функции в ряд Фурье. В данный ряд были разложены: функция, продолженная произвольным способом, функция, продолженная четным способом и функция, продолженная нечетным способом.
Были построены графики сумм гармоник функций, которые показали, что при увеличении количества гармоник, графики частичных сумм становятся все ближе к графику исходной функции. Следовательно, средняя квадратическая ошибка уменьшается при увеличении числа гармоник.
5. Используемая литература.
1) Романовский П.И., Ряды Фурье, Теория поля, Аналитические и специальные функции, Романовский П.И., Выпуск 3, Избранные главы высшей математики для инженеров и студентов ВТУЗов, 1961г., 306с.
2)Соболев А.Б., Рыбалко А.Ф., Вараксин А.Н. Математика: курс лекций для технических вузов. Кн.2.М.: Академия, 2010.-448с.
3) Колобов А.М., Ряд Фурье, Интеграл Фурье, Операционное исчисление, Колобов А.М., Часть 1, Избранные главы высшей математики, 1965г., 226с.
4 Жевняк Р.М., Карпук А.А. Высшая математика. Ч. III. Минск: Высшая школа,185.-208с.
5) Власов Е.А. Ряды. М.: МГТУ им. Н.Э. Баумана, 2000.-612с.
