Курсовая работа:

“Гармонический анализ функции”.

Группа: 7о-109с

Вариант: 12

Автор: Шишлянников Н.Ю.

Содержание:

1.Введение.

2.Теоритическая часть.

2.1 Гармонический анализ.

2.2 Ортогональные системы функций.

2.3 Тригонометрический ряд Фурье.

2.4 Теорема Дирихле о достаточных условиях разложения функции в ряд Фурье.

2.5 Разложение различных видов функций в ряд Фурье.

2.6 Средняя квадратическая ошибка представления функции рядом Фурье.

2.7 Амплитудный и фазовый спектры периодической функции.

2.8 Достаточные условия представления функции интегралом Фурье.

3.Практическая часть.

4.Заключение.

5.Список используемой литературы.

Задание на курсовую работу:

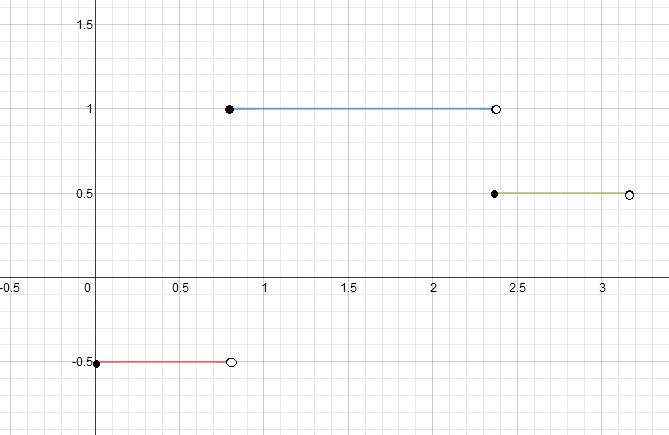
1. Функцию f(x), заданную графически на промежутке (0;π), описать аналитически.

2. Продолжить функцию f(x) произвольным, четным и нечетным способами на промежутке (-π;0), и построить графики периодически продолженных функций.

3. Проверить достаточные условия разложения периодически продолженных функций в тригонометрический ряд Фурье.

4. Найти коэффициенты Фурье и представить периодически продолженные функции рядом Фурье соответственно общего вида, по косинусам и по синусам.

5. Определить значения разложения функции в точках разрыва и на концах периодов.

6. Для всех трех случаев разложения функции построить графики сумм

• 0-й и 1-й гармоник,

• 0-й, 1-й и 2-й гармоник,

• 0-й, 1-й, 2-й и 3-й гармоник,

любого (большого) числа гармоник

ряда Фурье, которые совместить с графиками периодически продолженных функций.

7. Вычислить средние квадратические ошибки представления периодически продолженных функций рядом Фурье общего вида, по косинусам и по синусам.

8. Для всех трех случаев разложения функции в ряд Фурье определить амплитудные спектры и построить их графики.

9. Продолжить функцию f(x) произвольным, четным и нечетным способами на промежутке (-π,0) и нулевыми значениями вне промежутка (-π,π).

10. Проверить достаточные условия представления продолженных функций интегралом Фурье.

11. Представить продолженные функции интегралом Фурье и построить их графики.

График:

1.Введение

Универсальность гармонического колебания заключается также в том, что любой периодический сигнал может быть составлен (в этом случае говорят: синтезирован) только из гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Раздел теории сигналов, который занимается разложением сигналов на гармонические составляющие, называется гармоническим анализом сигналов или Фурье-анализом. Основные положения этой теории заключаются в следующем.

Любой периодический сигнал с периодом Т может быть представлен суммированием определенного набора гармонических колебаний с круговыми частотами, равными ωn=nω1= =2πn/T, где n - номер гармоники (натуральное число). При этом гармонику с номером n = 1 называют основной гармоникой, а гармоники с номерами n > 1 - высшими гармониками. В общем случае количество таких гармоник может быть бесконечным.

2.Теоретическая часть.

2.1 Гармонический анализ

Гармони́ческий ана́лиз (или Фурье́-ана́лиз) — раздел математики, в котором изучаются свойства функций с помощью представления их в виде рядов или интегралов Фурье. Также метод решения задач с помощью представления функций в виде рядов или интегралов Фурье.

2.2 Ортогональные системы функций

Скалярным произведением двух функций f (x) и ϕ(x), определенных и кусочно непрерывных на [a; b] называется число, обозначаемое ( f (x),ϕ(x)), и равное определенному интегралу от произведения этих функций по отрезку [a; b], т.е.

( f (x),ϕ(x))=

Функции f (x) и ϕ(x) называются ортогональными на [a;b] если их скалярное произведение равно нулю, т.е. если

=0

Нормой функции f (x) на [a; b] называется число, обозначаемое ||f (x)|| и равное корню квадратному из интеграла 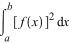,т.е ||f(x)||= .

Если интеграл то функция f(x) называется нормированной на [a; b].

Последовательность функций )} { f (x i называется ортогональной на [a; b], если любые две различные функции этой системы ортогональны на [a; b], т.е

,

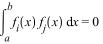Последовательность функций{ }называется нормированной на [a; b], если нормирована каждая функция этой последовательности, т.е.

,

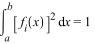Последовательность функций{ }называется ортонормированной на [a; b], если она является ортогональной и нормированной, т.е

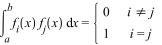
Ортогональную (ортонормированную) систему функций можно считать аналогом ортогонального (ортонормированного) базиса в конечномерном евклидовом пространстве. Как мы позднее убедимся, имеется класс функций, которые являются линейными комбинациями функций ортогональной (ортонормированной) системы, причем слагаемых в линейной комбинации может быть бесконечное число. Линейная комбинация с бесконечным числом слагаемых представляет собой ряд. Использование ряда как функции связано с вопросами сходимости этого ряда.