2.4. Методы анализа основной тенденции развития в рядах динамики

Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления.

В некоторых случаях закономерность изменения явления, об­щая тенденция его развития явно и отчетливо отражаются уровня­ми динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются).

Однако часто приходится встречаться с такими рядами дина­мики, в которых уровни ряда претерпевают самые различные из­менения, (то возрастают, то убывают) и общая тенденция разви­тия неясна.

Поэтому при анализе динамики речь идет не просто о тенден­ции развития, а об основной тенденции, достаточно стабильной (ус­тойчивой) на протяжении изученного этапа развития.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Задача состоит в том, чтобы выявить общую тенденцию в изме­нении уровней ряда, освобожденную от действия различных слу­чайных факторов. С этой целью ряды динамики подвергаются об­работке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество ин­тервалов). Например, ряд ежесуточного выпуска продукции заменя­ется рядом месячного выпуска продукции и т.д. Средняя, исчис­ленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

Рассмотрим применение метода укрупнения интервалов из ежемесячных данных о выпуске продукции на предприятии в 2012 г. (табл. 2).

Таблица 2

Объем производства продукции предприятия (по месяцам) в сопоставимых ценах, млн. руб.

Месяц	Объем производства	Месяц	Объем производства
Январь. Февраль Март Апрель Май Июнь	5,1 5,4 5.2 5,3 5,6 5,8	Июль Август Сентябрь Октябрь Ноябрь Декабрь	5,6 5,9 6,1 6,0 5,9 6,2

Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в кварталь­ные и вычислить среднемесячный выпуск продукции по кварталам (табл. 3), т.е. укрупнить, интервалы, то решение задачи упрощается.

Таблица 3

Объем производства продукции предприятия (по кварталам) в сопоставимых ценах, руб.

Квартал	За квартал	В среднем за месяц
I	15.7	5,23
II	16,7	5,57
III	17.6	5,87
IV	18,1	6,03

После укрупнения интервалов основная тенденция роста произ­водства стала очевидной: 5,23 < 5,57 < 5,87 < 6,03 млн руб.

Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его за­ключается в том, что исчисляется средний уровень из опреде­лимого числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем — из такого же числа уровней, но начиная со второго по счету, далее - начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок.

Расчет скользящей средней рассмотрим на примере данных об урожайности зерновых культур в одном из регионов РФ, (табл. 4).

Таблица 4

Исходные данные и результаты расчета скользящей средней, ц/га

Год	Урожайность зерновых, ц/га, Уi	Трехлетние скользящие суммы Σ Уi	Трехлетние скользящие средние
2003	15,4 (У1)	-	-
2004	14,0 (У2)	47,0 (У1 + У2 + У3 )	15,7
2005	17,6 (У3)	47,0 (У2 + У3 + У4)	15,7
2006	15,4	43,9	145
2007	10,9	43,8	14,6
2008	17,5	43,4	14,5
2009	15,0	51,0	17,0
2010	18,5	47,7	15,9
2011	14,2	47,6	15,9
2012	14,9	-	-

Сглаженный ряд по трехлетиям короче фактическо­го на один член ряда в начале и в конце, по пятилетиям — на два члена в начале и конце ряда и меньше, чем фактический, подвер­жен колебаниям из - за случайных причин и четче выражает основную тенденцию развития за изучаемый период.

Рассмотренные приемы сглаживания динамических рядов (ук­рупнение интервалов и метод скользящей средней) дают возмож­ность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колеба­ний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчи­тывается как функция времени:

,

где - уровни динамического ряда, вычисленные по соответствующе­му аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней , произво­дится на основе так называемой адекватной математической моде­ли, которая наилучшим образом отображает (аппроксимирует) ос­новную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер раз­вития явления, а также на графическом изображении ряда динами­ки (линейной диаграмме).

Например, простейшими моделями (формулами), выражающими тенденцию развития являются:

• линейная функция — прямая

где a_0, a₁— параметры уравнения; t — время;

• показательная функция

• степенная функция — кривая второго порядка (парабола)

Расчет параметров функции обычно производится методом наи­меньших квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретиче­скими и эмпирическими уровнями:

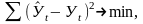
- выровненные (расчетные) уровни; У_i - фактические уровни.

Параметры уравнения a_i , удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выравненные уровни ряда.

Таким образом, выравнивание ряда динамики заключается в замене фактических уровней У_i плавно изменяющимися уровнями , наилучшим образом аппроксимирующими статистические данные.

Рассмотрим применение аналитического выравнивания на основании исходных данных табл. 4.

Таблица 5

Выравнивание по прямой ряда динамики урожайности зерновых культур по одному из регионов РФ, ц/га

Годы	Урожай-ность зерновыхкультур ц/га, Уi	t	t 2	уt	Теорети-ческий уровень		( )2
2003	15,4	- 9	81	-138,6	15,15	0,25	0,0625
2004	14,0	- 7	49	- 98,0	15,19	-1,19	1,4161
2005	17,6	- 5	25	- 88,0	15,23	2,37	5,6169
2006	15,4	- 3	9	- 46,2	15,28	0,12	0,0144
2007	10,9	- 1	1	- 10,9	15,32	-4,42	19,5364
2008	17,5	+1	1	17,5	15,36	2,14	4,5796
2009	15,0	+ 3	9	45,0	15,40	-0,40	0,0160
2010	18,5	+ 5	25	92,5	15,45	3,05	9,3025
2011	14,2	+ 7	49	99,4	15,49	-1,29	1,6641
2012	14,9	+ 9	81	134,1	15,53	-0,63	0,3969
Итого	153,4	0	330	6,8	153,4	0	42,6054

Выравнивание данного динамического ряда произведем по уравнению прямой линии:

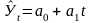
В нашем примере n=10.

Параметры a_0, a₁ согласно методу наименьших квадратов находят решением следующей системы нормальных уравнений:

Σу =na₀+a₁Σt,

Σуt=a₀Σt +a₁Σt²

Для упрощения нахождения параметров уравнения при сохранении полной идентичности конечных результатов введем обозначения дат или периодов времени с натуральным числом (t), с тем, чтобы t=0.

Так как Σt= 0 (мы предполагаем), то система нормальных уравнений примет вид:

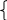Σу=na₀,

Σуt=a₁Σt².

Отсюда: , ;

, .

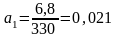Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид:

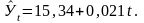
Подставив в данное уравнение последовательно значения t , равные –9, -7, -5, -3, -1, +1,+3, +5, +7, +9, находим выровненные уровни .

Подставив в это уравнение значение t, получаем выравненные теоретические

значения

Если расчеты выполнены правильно, то 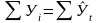. В нашем примере = 153,4. Следовательно, значения уровней выравненного ряда найдены верно.

Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 2003 по 2012 гг., т.е. урожайность зерновых культур в среднем возрастала на a₁= 0,021 ц/га в год.

Фактические и расчетные значения урожайности представлены в виде графика (см. рис. 1).

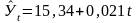
Рис.1. Динамика урожайности зерновых культур за 2003 – 2012 гг.

-------- Первичный динамический ряд;

______ Выравненный динамический ряд.

Соединив точки, построенные по фактическим данным, получим ломаную линию, на основании которой затруднительно вынести суждение о характере общей тенденции динамики в изменении урожайности.

Тенденция роста урожайности зерновых культур в изученном периоде отчетливо проявляется в результате построения выравненной прямой.

Выявление и характеристика трендов создают базу для прогнозирования, т.е. для определения ориентировочных размеров явлений в будущем. Для этого используют метод экстраполяции.

Под экстраполяцией понимают нахождение уровней за пределами изучаемого ряда, т.е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция).

Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней, и подставляя в него значения t за пределами исследуемого ряда, рассчитывают для t вероятностные .

Так по данным табл. 5, на основе исчисленного ранее уравнения экстраполяцией при t=11 можно определить ожидаемую урожайность зерновых культур в 2013, ц/га:

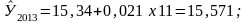
На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками.

Для определения границ интервалов используют формулу:

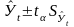
где - коэффициент доверия Стьюдента;

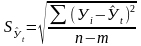- остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n-m);

n- число уровней ряда динамики;

m- число параметров адекватной модели тренда (для уравнения прямой m=2).

Вероятностные границы интервала прогнозируемого явления:

Рассчитаем прогнозируемые доверительные интервалы урожайности зерновых культур на 2013 год.

Если n=10 и m=2, то число степеней свободы равно 8. Тогда при доверительной вероятности равной 0,95 (т.е. при уровне значимости случайностей 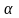= 0,05), коэффициент доверия (по таблице Стъюдента), (см. табл. 5).

Тогда _.

Зная точечную оценку прогнозируемого значения урожайности ц/га, определяем вероятностные границы интервала:

15,571 –2,306 х 2,308 15,571+2,306 х 2,308;

10,25 20,89.

Следовательно, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в 2013 г. будет не менее чем 10,25, но не более чем 20,89 ц/га.

Список рекомендуемой литературы

1. Афанасьев В.Н., А.И. Макарова. Статистика сельского хозяйства : Учебное пособие для вузов. М: Финансы и статистика, 2003.

2. Башкатов Б.И. Статистика сельского хозяйства с основами общей теории статистики: Курс лекций. М.: Тандем: ЭКМОС, 2001.

3. Годин А.М. Статистика: Учебник. М.: Издательство - торговая корпорация «Дашков и К⁰ », 2007.

4. Голуб Л.А. Социально-экономическая статистика : Учебное пособие. М.: ВЛАДОС, 2003.

5. Гусаров В.М. Статистика: Учебное пособие для вузов. М.: ЮНИТИ, 2006.

6. Гришин А.Ф. Статистика : Учебное пособие для вузов по агр. и эконом. спец. М.: Финансы и статистика, 2003.

7. Зинченко А.П. Практикум по статистике. М. : Колос, 2004.

8. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник – 5-е изд., перераб. и доп. М.: Финансы и статистика, 2006.

9. Ефимова М.Р., Бычкова С.Г. Социальная статистика : Учебное пособие. М.: Финансы и статистика, 2004.

10. Общая теория статистики: Учебник /Под ред. Башиной О.Э., Спирина А.А. – 5-е изд. доп. и перераб. М.: Финансы и статистика, 2004.

11. Курс социально – экономической статистики : Учебник /Под ред. Назарова М.Г.- 6-е изд. испр. и доп. М.: Омега – Л, 2007.

12. Макроэкономическая статистика: Учебное пособие для вузов / Под ред. Салина В.Н. М.: Дело, 2000.

13. Рудакова Р.П., Букин Л.Л. , Гаврилов В.И. Статистика : Учебное пособие. 2-е изд. – СПб: Питер, 2007.

14. Салин В.Н., Шпаковская Е.П. Социально – экономическая статистика : Учебник. М.: Финансы и статистика, 2001.

15. Салин В.Н., Шпаковская Е.П. Социально – экономическая статистика : Практикум. М.: Финансы и статистика, 2004.

16. Статистика: Учебник / Под ред. Елисеевой И.И. М.: Проспект, 2006.

17. Статистика: Учебник/ Под ред. Елисеевой И.И.. М.: Высшее образование, 2006.