1. Множества и операции над множествами.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами   , а элементы множества строчными латинскими буквами   .

Запись   означает, что есть множество   с элементами  , которые связаны между собой какой-то функцией   .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

1. Принадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   принадлежит множеству   ).

2. Непринадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   не принадлежит множеству   ).

3. Объединение множеств:   .

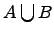Объединением двух множеств   и   называется множество   , которое состоит из элементов множеств   и   , т.е.

   или

4. Пересечение множеств:   .

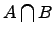Пересечением двух множеств   и   называется множество   , которое состоит из общих элементов множеств   и   , т.е.

   и

5. Разность множеств:   .

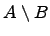Разностью двух множеств   и   , например, множество   минус множество   , называется множество   , которое состоит из элементов множества   , которых нет в множестве   , т.е.

   и

6. Симметрическая разность множеств:   .

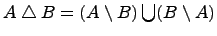Симметрической разностью двух множеств   и   называется множество   , которое состоит из не общих элементов множеств   и   , т.е.

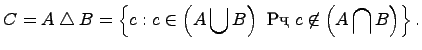
7. Дополнение множества:   .

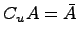Если предположим, что множество   является подмножеством некоторого универсального множества   , тогда определяется операция дополнения:

   и

8. Вхождение одного множества в другое множество:   .

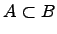Если любой элемент множества   является элементом множества   , то говорят, что множество   есть подмножество множества   (множество   входит в множество   ).

9. Не вхождение одного множества в другое множество:   .

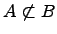Если существует элемент множества   , который не является элементом множества   , то говорят, что множество   не подмножество множества   (множество   не входит в множество   ).

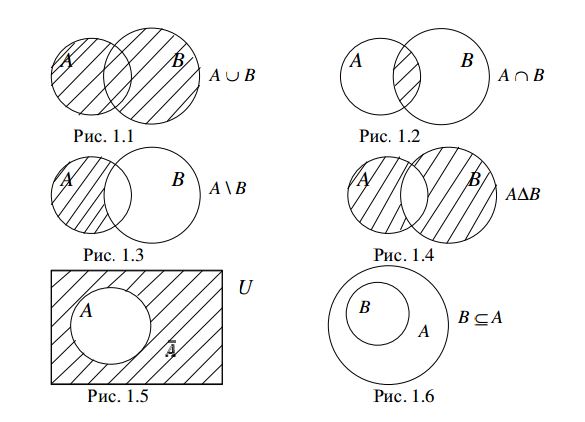
2. Круги Эйлера

Для графического (наглядного) изображения множеств и их свойств ис-

пользуются диаграммы Эйлера – Венна (Леонард Эйлер (1707–1783) – швей-

царский математик, механик и физик; Джон Венн (1834 – 1923) – английский

логик). На них множество отождествляется с множеством точек на плоскости,

лежащих внутри некоторых замкнутых кривых, например окружностей (так на-

зываемые круги Эйлера). В частности, универсальное множество U изобража-

ется множеством точек некоторого прямоугольника.

Проиллюстрируем с помощью диаграмм Эйлера – Венна введенные оп-

ределения. На рисунках 1.1 – 1.5 результат выполнения операции выделен

штриховкой.

3. Бинарные отношения, виды бинарных отношений:

N-арным (n-местным) отношением P на множествах

A1, A2, …, An называется любое подмножество прямого произведения

A1 × A2 × …× An.

В случае n = 1 отношение P называется унарным (одноместным) и явля-

ется подмножеством множества A1.

При n = 2 P называется бинарным (двуместным) отношением или соот-

ветствием. Если P ⊆ A1 × A2

, то также говорят, что Р есть отношение между

множествами A1 и A2 (между элементами множеств A1 и A2 ) или что Р задано

(определено) на паре множеств A1 и A2. Если A1 = A2 = A ( P ⊆ A × А ), то гово-

рят, что Р есть бинарное отношение на множестве А.

Пусть Р – бинарное отношение и (x, y) ∈ P, тогда говорят, что элемент x

находится в отношении P к элементу y, или что x и y связаны отношением P.

Вместо записи (x, y) ∈ P часто пишут xPy.

Виды бинарных отношений

Бинарные отношения называются рефлексивными, если  (a_i ) A (a_i ,a_i )  .

Если отношение является рефлексивным, то в его таблице на главной диагонали стоят единицы.

Бинарное отношение антирефлексивно, если  (a_i ) A (a_i ,a_i )   .

В антирефлексивном отношении главная диагональ не содержит ни одной единицы.

Бинарные отношения называются симметричными , если  (a_i,a_j)  (a_j ,a_i )  .

Для симметричного отношения таблица симметрична относительно главной диагонали.

Бинарное отношение антисимметрично, если из того, что (a_i,a_j)  , следует, что(a_j ,a_i )  .

Бинарные отношения называются транзитивными, если из того, что (a_i ,a_j ) и (a_j ,a_k )   , (a_i ,a_k )  .

4. Графы. Способы задания. Виды графов.

 Граф G=(V,E) определяется как совокупность двух (как правило, конечных) множеств: множества V точек, называемых вершинами, и множества E линий, соединяющих точки, называемых ребрами. Каждое ребро может быть инцидентно (присоединено к) ровно двум вершинам. Это позволяет задавать ребра парами инцидентных ему вершин. Если ребра определяются как упорядоченные пары вершин, то граф называется ориентированным графом (орграфом); ребра в этом случае называют дугами; первую вершину пары называют началом дуги и считают, что из нее дуга выходит, а вторую - концом дуги и считают, что в нее дуга заходит. Если же порядок вершин в парах, описывающих ребра графа, не имеет значения, граф называют неориентированным графом (неорграфом). Вершины, соединенные ребром или дугой, называют смежными вершинами.

виды графов. Графически вершины графа обычно изображают точками или окружностями, а ребра - соединяющими их линиями. Направленность дуг в ориентированных графах указывают стрелками. Мы будем изображать вершины как точками, так и окружностями с надписями, когда будет возникать необходимость различать вершины между собой.

Если множество E ребер графа пусто граф называется пустым. Если пусто не только множество E ребер, но и множество V вершин графа, граф называется нуль-графом. Пустой граф, имеющий лишь одну вершину, называется тривиальным графом.

Ребро графа, соединяющее вершину саму с собой, называют петлей. Петля, как и всякое другое ребро, может быть ориентированной или неориентированной (рис. 1.1, б).

Одной и той же паре вершин в графе может быть инцидентно несколько ребер (рис.1.1, г). Такие ребра называют кратными, а граф, содержащий кратные ребра, часто называют мультиграфом. В ориентированном графе дуги считаются кратными, если они однонаправленны.

Граф не содержащий петель и кратных ребер (рис. 1.1, в), называют простым. Такой же смысл вкладывается в этот термин в случае ориентированных графов (рис. 1.1, д и рис. 1.1, е).

Обычно рассматривают конечные графы, но иногда приходится рассматривать и бесконечные графы (как, например, на рис. 1.1, д). В этом случае граф определяется некоторой процедурой или правилом порождения бесконечных множеств его вершин и ребер.

Принято считать, что неориентированному графу соответствует ориентированный граф с тем же множеством вершин, в котором каждое неориентированное ребро исходного графа заменено двумя противоположно направленными дугами. Такое соответствие между неорграфом и орграфом называют каноническим (каноническим представлением графа на рис. 1.1, в является граф на рис. 1.1, е). Граф может содержать одновременно как ребра, так и дуги. Получение канонического представления такого графа сводится к замене ребер двумя противоположно направленными дугами без изменения имевшихся дуг. Например, графом такого типа будет изображение вершинами населенных пунктов и развилок дорог, а ребрами и дугами – дорог, соответственно, с двусторонним и односторонним движением.

С п о с о б ы      з а д а н и я    г р а ф о в

Задать граф - значит описать множество его вершин, множество ребер и отношение инцидентности вершин и ребер. Кроме графического представления, наиболее употребительны также описания графов с помощью матриц инциденций, списков ребер, матриц смежности вершин и посредством отображений.

Матрица инциденций. Если граф конечен, для его описания достаточно указать список вершин V={v₁,….,v_n}, список ребер E={e₁,….,e_m} и матрицу инциденций  . Элементы матрицы инциденций неориентированного графа определяются следующим образом:

В матрицах инциденций ориентированных графов используются дополнительные символы для отражения направленности дуг. Например, часто применяется следующая нотация элементов матрицы инциденций:

На рис. I.2, б и рис. I.3, б приведены примеры матриц инциденций неорграфа и орграфа, изображенных, соответственно, на рис. I.2, а и рис. I.3, а.

Список ребер. Как видно из определения и примеров, каждый столбец матрицы инциденций содержит не более двух ненулевых элементов, что при компьютерной обработке больших графов требует много лишней памяти компьютера. В таких случаях часто граф описывают списком ребер, каждое из которых представляется парой вершин. В неорграфах порядок вершин не имеет значения и не учитывается. В орграфах первой в паре указывается вершина, являющаяся началом дуги, а второй - вершина, являющаяся ее концом. На рис. I.2, г и рис. 1.3, г представлены списками ребер выше уже упомянутые графы, изображенные на рис. I.2, a и на рис. 1.3, a.

Матрица смежности. Для выполнения над графами алгебраических операций удобно описание графов матрицами смежности вершин. Матрица смежности вершин графа - это квадратная матрица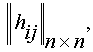 строки и столбцы которой соответствуют вершинам графа, а каждый ее элемент h_ij равен числу дуг из вершины v_i в вершину v_j. Таким образом, для неорграфа матрица смежности вершин симметрична относительно главной диагонали и, по сути, выражает каноническое представление неорграфа орграфом. Для орграфа свойство симметрии матрицы смежности вершин, как правило, не имеет места. На рис. 1.2, в и рис. 1.3, в даны матрицы смежности вершин неорграфа и орграфа, представленных графически на рис. 1.2, а и рис. 1.3, а, соответственно.

Рис. 1.2. Способы представления неорграфа: а - графический; б - матрицей инциденций;  в - матрицей смежности вершин; г - списком ребер

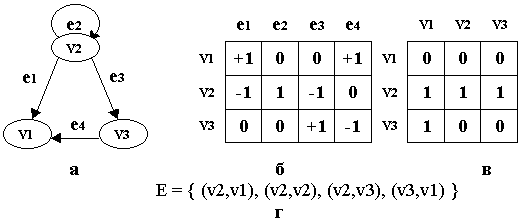  Рис. 1.3. Способы представления орграфа:  а - графический; б - матрицей инциденций;  в - матрицей смежности вершин; г - списком ребер (дуг)

5. Подграфы

Определение 2 (Подграф). Подграфом графа называется граф, являющийся подмоделью исходного графа. Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).

Определение 3 (Подграф, порождённый множеством вершин).

Подграфом, порождённым множеством вершин U называется подграф, множество вершин которого – U, содержащий те и только те рёбра, оба конца которых входят в U.

Определение 4 (Остовной подграф). Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа.

Два последних определения дают два вида максимальности подграфов: максимальность множества вершин и максимальность множества рёбер.

Граф H называется подграфом графа G  (пишут: H ⊆ G),  если  V(H) ⊆ V(G)  и E(H) ⊆ E(G). Если для подграфа H графа G  V(H)=V(G), то H называется остовным подграфом.

Если подграф H содержит все рёбра графа G, оба конца которых принадлежат множеству U ⊂ V(G), то H называется подграфом порождённым (индуцированным) множеством вершин U. Такой подграф H  обозначается: G(U).

Рассматриваются также подграфы, порождённые данным подмножеством  рёбер графа G, которые вместе с указанными рёбрами содержат все их концы в качестве множества вершин.

Важным классом подграфов являются подграфы, полученные из данного графа G удалением некоторой вершины v (при этом удаляются также все рёбра, инцидентные v). Обозначение полученного подграфа: Gv. Понятно, что Gv = G(V(G)\{v}).

Для графа G на следующем рисунке приведены примеры вышеуказанных подграфов:

Операции над графами Удаление вершин (см. выше). Удаление ребра (при этом концы ребра не удаляются), а также добавление ребра. Другие переходы к подграфам или надграфом. Дополнение графа.  Граф     называется дополнением графа  G,  если V( ) = V(G), причём вершины u и v являются смежными в графе  тогда и только тогда, когда они не смежны в G.  Таким образом,  G и   не имеют общих рёбер, а E(G) ∪ E( ) с общим множеством вершин образует полный граф. Объединение графов.

Объединением графов G1  и G2 называется граф G1∪G2, в котором V(G1∪G2) = =V(G1)∪V(G2)  и  E(G1∪G2) = E(G1)∪E(G2).

Пересечение графов.

Пересечением графов G1 и G2 называется граф G1∩G2, в котором V(G1∩G2) = =V(G1)∩V(G2)  и  E(G1∩G2) = E(G1)∩E(G2).

Соединение графов.

Соединением графов G1 и G2 называется объединение G1∪G2, дополненное всеми рёбрами, соединяющими вершины G1 с вершинами G2. Обозначается соединение: G1+G2,

В частности, если Gi  – (ni, mi)-графы, не имеющие общих вершин, то G1+G2 будет (n1+n2, m1+m2+n1⋅n2)-графом. Так, например,  Kp,q = 0p+ 0q =   + .

Рассматриваются также другие более сложные операции на графах, такие как, произведение графов, прямое произведение и др.

6. Остов

Граф без циклов называется ациклическим или лесом.

Связный ациклический граф называется деревом.

Если G-лес, то каждая его компонента является деревом.

Остов графа – это дерево, являющееся остовным подграфом.

Остовной подграф – это подграф, множество вершин которого совпадает с множеством вершин графа.

Любой связный граф имеет остов. Обратно, если граф имеет остов, то он – связный.

Если граф имеет циклы, то, последовательно удаляя ребра из циклов до получения ациклического подграфа, получим остов. Причем, удаление ребра из цикла графа не нарушает его связности, т.к. такие ребра не являются мостами.

Ребро x и вершина v называются покрывающими друг друга, если они инцидентны. Множество вершин, покрывающих все ребра, называется вершинным покрытием графа. Множество ребер, покрывающих все вершины, называется реберным покрытием графа. Представляет интерес наименьшие по числу вершин и ребер покрытия. Если ребрам графа приписаны веса, то можно ставить вопрос о реберном покрытии, имеющем наименьший суммарный вес.

Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины. Неформально говоря, остовное дерево состоит из некоторого подмножества рёбер графа, таких, что из любой вершины графа можно попасть в любую другую вершину, двигаясь по этим рёбрам, и в нём нет циклов, то есть из любой вершины нельзя попасть в саму себя, не пройдя какое-то ребро дважды.

Понятие остовный лес неоднозначно, под ним могут понимать один из следующих подграфов:

• любой ациклический подграф, в который входят все вершины графа, но не обязательно связный;

• в несвязном графе — подграф, состоящий из объединения остовных деревьев для каждой его компоненты связности.

Остовное дерево также иногда называют покрывающим деревом, остовом или скелетом графа. Ударение в слове «остовный» у разных авторов указывается на первый^[1] (от слова о́стов) или на второй слог.

Свойства [править]

• Любое остовное дерево в графе с 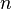  вершинами содержит ровно 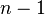  ребро.

• Число остовных деревьев в полном графе на   вершинах выражается знаменитой формулой Кэли:^[2]

• В общем случае, число остовных деревьев в произвольном графе может быть вычислено при помощи так называемой матричной теоремы о деревьях.

7. Алгоритм нахождения расстояния между вершинами графа

Пусть вершины графа   пронумерованы от 1 до   и введено обозначение   для длины кратчайшего пути от  до  , который кроме самих вершин   проходит только через вершины  . Очевидно, что   — длина (вес) ребра  , если таковое существует (в противном случае его длина может быть обозначена как  ).

Существует два варианта значения  :

1. Кратчайший путь между   не проходит через вершину 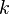 , тогда 

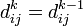
2. Существует более короткий путь между  , проходящий через  , тогда он сначала идёт от   до  , а потом от   до  . В этом случае, очевидно, 

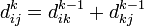
Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений.

Тогда рекуррентная формула для   имеет вид:

 — длина ребра 

Алгоритм Флойда-Уоршелла последовательно вычисляет все значения     для   от 1 до  . Полученные значения   являются длинами кратчайших путей между вершинами 

8. Нахождение минимального остова

?

Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

9. Эйлеров граф

Эйлеровы графы

Эйлеров граф — граф, содержащий эйлеров цикл.

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

Эйлеровым называется цикл, проходящий по каждому ребру графа ровно один раз. Граф, имеющий эйлеров цикл, тоже будем называть эйлеровым.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Теорема (критерий эйлеровости графа): граф является эйлеровым тогда и только тогда, когда степени всех его вершин – чётные числа.  Требование связности в теореме естественно – несвязный граф может быть эйлеровым только в том случае, если только одна связная компонента содержит рёбра.  В неориентированном графе : согласно теореме, доказанной Эйлером, эйлеров цикл существует тогда и только тогда, когда граф связный и в нём отсутствуют вершины нечётной степени. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечётной степени.  Ввиду леммы о рукопожатиях, число вершин с нечётной степенью должно быть четным. А значит Эйлеров путь существует только тогда, когда это число равно нулю или двум. Причём когда оно равно нулю, эйлеров путь вырождается в эйлеров цикл.  В ориентированном графе: граф содержит эйлеров цикл тогда и только тогда, когда он сильно-связан и для каждой вершины графа её полустепень захода равна её полустепени исхода, то есть в вершину входит столько же ребер, сколько из неё и выходит.

Поиск эйлерова пути в графе:

Можно всегда свести задачу поиска эйлерова пути к задаче поиска эйлерова цикла. Действительно, предположим, что эйлерова цикла не существует, а эйлеров путь существует. Тогда в графе будет ровно 2 вершины нечётной степени. Соединим эти вершины ребром, и получим граф, в котором все вершины чётной степени, и эйлеров цикл в нём существует. Найдём в этом графе эйлеров цикл), а затем удалим из ответа несуществующее ребро.

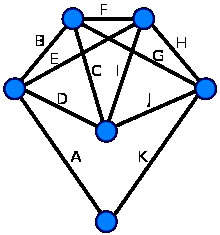
Каждая вершина этого графа имеет чётную степень, поэтому этот граф — эйлеров. Обход рёбер в алфавитном порядке даёт эйлеров цикл.

10. Гамильтонов граф.

Граф называется гамильтонов – если в нем существует цикл проходящий через все вершины графа по одному разу.

Теорема: Если для любых двух различных не смежных вершин a и b выполняется условие, то в графе существует гамильтонов цикл.

Алгоритм Роберта – Флоренса: позволяет найти все гамильтоновы циклы графа. 1. Составляем список смежности: в столбцах соответсвующих вершинам перечисляем вершины смежные с данной вершиной.

2. S = {a}

3. Из столбца последняя вписанная в с вершина выбираем первую возможную вершину и вписываем ее в S

Возможная вершина – первая после удаленной на последующем шаге уже построенного пути S.

4. Если нет таких вершин:

А) то все вершины включены в S. Если последняя совпадает с первой, то посроим гамильтонов цикл.

Б) Если не все вершины включены, то возвращаемся на шаг назад и удаляем последнюю включенную вершину.

11. Потоки в сетях

Сетью называется связный граф (обычно, не орграф и не мультиграф), в котором заданы “пропускные способности” ребер, т. е. числа q_ij. Это числа большие или равные нулю, причем q_ij = 0 тогда и только тогда, когда нет ребра, соединяющего вершины i и j. Таким образом, можно считать, что пропускные способности ребер заданы для любой пары вершин. В дискретной математике пропускные способности ребер, как и все возникающие константы, считаются целыми числами (или рациональными, что одно и то же, так как рациональные числа отличаются от целых только единицами измерения).

Потоком в сети между вершиной t (источником) и s (стоком) называется набор чисел с_ij, (т. е. количество условного “груза”, перевозимого из вершины с номером i в вершину с номером j), удовлетворяющих четырем условиям:

1) числа с_ij   0, причем если с_ij > 0, то с_ji = 0 (нет встречных перевозок);

2) числа c_ij   q_ij (соответствующих пропускных способностей ребер);

3) если вершина с номером i – промежуточная (не совпадает с источником и стоком), то

,

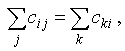
т. е. количество “груза”, вывозимого из вершины i, равно количеству “груза”, ввозимого в эту вершину;

4)  количество “груза”, вывозимого из источника t, должно быть равно количеству груза, ввозимого в сток s:

.

Число А называется величиной данного потока или просто потоком между t и s.

Для дальнейшего нам нужно следующее определение:

Пусть имеется некоторое сечение между вершинами t и s. Тогда величиной сечения называется сумма пропускных способностей ребер, входящих в это сечение. Сечение называется минимальным (максимальным), если его величина минимальна (максимальна).

12. Задача о максимальном потоке: