
- •1. Мова програмування. Класифікація мов програмування. Поняття про інтерпретацію та компіляцію. Інтегровані середовища програмування.
- •2. Загальна структура програми. Основні розділи програми і правила їх описання. Директиви препроцесора.
- •3. Поняття змінної. Оголошення змінної. Типи даних. Поняття локальних і глобальних змінних. Час життя змінної. Константи.
- •1. Char - символ
- •3. Float - число з плаваючою комою одинарної точності
- •4. Double - число з плаваючою комою подвійної точності
- •4. Поняття оператора. Різновиди операторів. Вирази. Основні правила запису, обчислення та використання виразів. Надання значень виразів змінним. Пріоритет операцій. Арифметичні операції,
- •5. Оператори введення та виведення: з використанням формату, символів, рядків.
- •Int printf (const char * керуючий_рядок, ...);
- •Int scanf (const char * керуючий_рядок, ...);
- •6. Вказівники та посилання. Адреси об’єктів в пам’яті. Динамічні структури даних.
- •7. Складені типи даних: масиви. Поняття масиву, одновимірні та багатовимірні масиви. Ініціалізація масивів та виведення їх на екран. Класичні алгоритми для роботи з масивами
- •8. Складені типи даних: рядки. Бібліотека функцій обробки рядків. Класичні алгоритми для обробки рядків
- •9. Складені типи даних: структури (записи)
- •10. Файлові типи даних. Файли прямого доступу.
- •11. Файлові типи даних. Файли послідовного доступу.
- •12. Алгоритмічна конструкція розгалуження та її графічне подання. Оператори розгалуження (умовний оператор та оператор вибору). Оператори зміни порядку виконання програми.
- •13. Алгоритмічна конструкція повторення та її графічне подання. Циклічні конструкції в мовах програмування. Оператори циклів. Оператори зміни порядку виконання програми.
- •14. Функціональний підхід в програмуванні. Рекурсія та її програмна реалізація.
- •15. Алгоритми пошуку: послідовний та бінарний пошук.
- •16. Алгоритм впорядкування : вибірка, вставка, обмін.
- •18. Абстрактні типи даних: лінійні списки
- •19. Абстрактні структури даних: стеки та черги
- •20. Абстрактні структури даних: двійкові дерева.
- •21. Наближені методи обчислення визначених інтегралів: метод лівих, правих та середніх прямокутників; метод трапецій; метод Сімпсона.
- •Метод Монте-Карло: зміст, приклади, застосування для обчислення площ складних фігур.
- •Наближені методи розв’язання алгебраїчних рівнянь: метод половинного ділення; метод хорд; метод дотичних.
- •Поняття моделювання та типи моделей. Класифікація моделей, інформаційна модель, математична модель як різновид інформаційної моделі. Основні етапи моделювання.
Метод Монте-Карло: зміст, приклади, застосування для обчислення площ складних фігур.
Метод Монте-Карло можна пояснити на задачі: Задано фігуру складної форми. Обчислити її площу.
Помістимо задану фігуру в квадрат. Будемо навмання (як кажуть математики, випадковим чином) «кидати» точки в цей квадрат. Природно припускати, що чим більша площа фігури, тим частіше в неї будуть попадати точки. Уявіть собі квадратний дворик і на ньому дитячу площадку. Кожному зрозуміло, що під час снігопаду кількість сніжинок, що потрапили на дитячу площадку, пропорційна її площі. Таким чином, можна зробити припущення: при більшій кількості точок, наугад вибраних всередині квадрату, частка точок, що містяться в даній фігурі, наближено рівна відношенню площі цієї фігури до площі квадрата.
Такий метод наближеного знаходження площ фігур має назву метод Монте-Карло.
Нескладно визначити, що в нашій моделі – початкові данні, а що – результат. Позначимо нашу фігуру буквою F. Вхідними даними є сторона a квадрата, що містить фігуру F, і кількість точок N, котрі ми будемо випадковим чином вибирати всередині квадрату. Результатом є площа S фігури F. Якщо через М позначити число тих, навмання вибраних точок, котрі містяться у фігурі F, то площа S наближено рівна a2M/N. Зрозуміло, що зв’язків між вхідними даними і результатом слід віднести і математичні співвідношення, які дають можливість визначити, чи потрапила вибрана точка в фігуру F.
Ці співвідношення будуть розрізняти моделі, побудовані для різних фігур. Значить, фактично ми описали не одну модель, а швидше – деякий спосіб отримання моделей. Для кожної фігури буде своя модель.
Давайте
розглянемо модель для наближеного
обчислення площі круга радіусу R.
Формула площі круга вам відома:
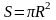 .
Перевіримо її за допомогою комп’ютера!
.
Перевіримо її за допомогою комп’ютера!
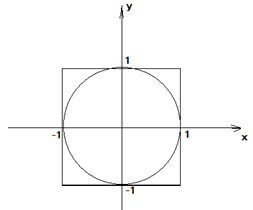
Нехай,
для певності, R=1.
На рисунку зображено круг радіусом 1,
обмежений квадратом зі стороною а=2.
Таким чином, фігура F
–
це круг одиничного радіусу. Вибрати
точку – це значить задати її координати:
числа x
та
y.
Точка належить квадрату, якщо
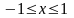 і
і
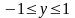 .
Якщо
.
Якщо
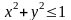 ,
то точка попадає в круг F,
інакше вона по за межами круга. Це і є
математичні співвідношення, що дають
змогу для кожної точки визначити, чи
належить вона F.
,
то точка попадає в круг F,
інакше вона по за межами круга. Це і є
математичні співвідношення, що дають
змогу для кожної точки визначити, чи
належить вона F.
Математична модель обчислення площі круга побудована. Приступимо до складання алгоритму розв’язку даної задачі. Випадкові числа будемо генерувати на Паскалі за допомогою стандартної функції Random, яка повертає дійсні числа з проміжку [0; 1). Вибирати точки будемо тільки в першій чверті (квадранті) координатної площини. Це на ймовірність попадання їх у круг не вплине, тому що частка площі, яку займає круг у квадраті однакова в усіх чотирьох менших квадратах, на які розбивають наш квадрат координатні осі.
Наближені методи розв’язання алгебраїчних рівнянь: метод половинного ділення; метод хорд; метод дотичних.
Метод
половинного деления. Разделим
отрезок [a, b] пополам точкой
c
=
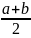 .
Если f(c)
.
Если f(c) (что практически наиболее вероятно), то
возможны два случая: либо f(x) меняет знак
на отрезке [a, c] (Рис. 1),
либо на отрезке [c, b] (Рис. 2)
(что практически наиболее вероятно), то
возможны два случая: либо f(x) меняет знак
на отрезке [a, c] (Рис. 1),
либо на отрезке [c, b] (Рис. 2)
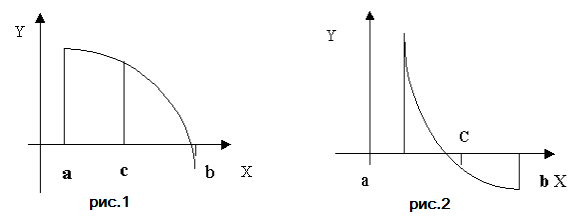
Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.
Метод хорд. Для реализации данного метода, нужно построить исходную функцию y=F(x) и найти значения функции на концах отрезка F(a) и F(b). Затем провести хорду М1M2 c концами в точках М1(a, F(a)) и M2(b, F(b)). Абсцисса точки пересечения хорды М1M2 с осью OX это и есть приближенный корень x1. Далее найти точку M3(X1 ,F(x1 )), построить следующую хорду и найти второй приближенный корень x2. И так далее. В зависимости от поведения функции возможны два случая:
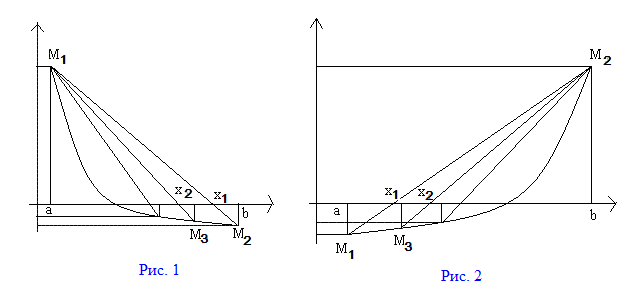
Для
первого случая (Рис. 1) справедлива
следующая формула:
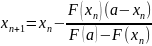 и справедливо неравенство: F(a)*F''(a)>0,
где x0=b.
и справедливо неравенство: F(a)*F''(a)>0,
где x0=b.
Для
второго случая (Рис. 2) справедлива
следующая формула: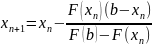 и справедливо неравенство: F(b)*F''(b)>0,
где x0=a.
Условия сходимости метода:
и справедливо неравенство: F(b)*F''(b)>0,
где x0=a.
Условия сходимости метода: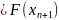 ≤ε
≤ε .
.
Метод
дотичних. В
методе касательных вместо хорды на
каждом шаге проводится касательная к
кривой y=F(x) при x=xn
и ищется точка пересечения касательной
с осью абсцисс: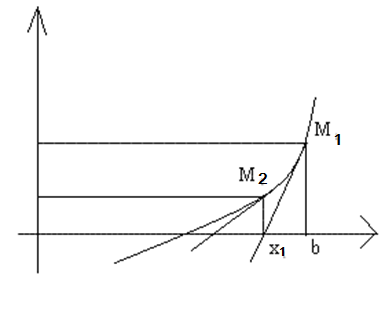
Формула
для (n+1) приближения имеет вид:
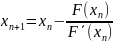 .
Если F(a)*F"(a)>0, x0=a, в противном случае
x0=b.
Итерационный
процесс продолжается до тех пор, пока
не будет обнаружено, что:
≤ε
.
.
Если F(a)*F"(a)>0, x0=a, в противном случае
x0=b.
Итерационный
процесс продолжается до тех пор, пока
не будет обнаружено, что:
≤ε
.
Точні та наближені методи розв’язання систем лінійних алгебраїчних рівнянь: матричний метод; розв’язання за формулою Крамера; метод Гауса; метод Жордана-Гауса; метод простої ітерації; метод Зейделя.
Метод Гауса. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Метод Зейделя. Для того щоб застосувати метод Зейделя для розв'язання системи лінійних алгебраїчних рівнянь Ax = b з квадратною не виродженою матрицею A, необхідно попередньо перетворити цю систему до вигляду x = Bx + c. Тут B - квадратна матриця з елементами bij (i, j = 1, 2, …, n), c - вектор-стовпчик з елементами cij (i = 1, 2, …, n). В розгорнутій формі запису система має наступний вигляд:
x1 = b11x1 + b12x2 + b13x3 + … + b1nxn + c1
x2 = b21x1 + b22x2 + b23x3 + … + b2nxn + c2
…………….
xn = bn1x1 + bn2x2 + bn3x3 + … + bnnxn + cn
Найпростіший спосіб зведення системи до вигляду, зручного для ітерацій, полягає в наступному: з першого рівняння системи виразимо невідоме x1,x2,…
В результаті отримаємо систему
x1 = b12x2 + b13x3 + … + b1,n-1xn-1 + b1nxn+ c1,
x2 = b21x1 + b23x3 + … + b2,n-1xn-1 + b2nxn+ c2,
x3 = b31x1 + b32x2 + … + b3,n-1xn-1 + b3nxn+ c3,
………………….
xn = bn1x1 + bn2x2 + bn3x3 + … + bn,n-1xn-1 + cn,в якій на головній діагоналі матриці B знаходяться нульові елементи.Інші елементи виражаються за формулами bij = - aij / aii, ci = bi / aii (i, j = 1, 2,., n ).
Метод Крамера. При вирішенні систем лінійних рівнянь за методом Крамера послідовно виконується наступний алгоритм:
1. Записують систему в матричному вигляді (якщо це ще не зроблено).
2. Обчислюють головний визначник.
3. Обчислюють всі додаткові визначники системи:
4.
Якщо головний визначник системи не
дорівнює нулю, то виконують пункт 5.
Інакше розглядають питання про можливість
розв'язання даної системи (має незліченну
безліч рішень або не має рішень). Знаходять
значення всіх невідомих за формулами
Крамера для розв'язання системи n лінійних
рівнянь з n невідомими, які мають вигляд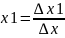 і
т.д.
і
т.д.
Метод простої ітерації.
Приведем решаемую систему Ax=b эквивалентным преобразованием к виду: x = C x + d. Это возможно сделать многими способами. Отсюда находим: C º E - HA, d º H b. Матрицу H нужно выбирать так, чтобы C обладала определенными свойствами, о которых будет сказано ниже (теорема). Итерационный процесс (то есть процесс последовательных приближений) метода простой итерации описывается формулой: x(k+1) = C x(k) + d, k = 0, 1, ...,где x(0) - некоторое начальное приближение к решению (обычно полагают x(0)=d).
В координатной форме метод простой итерации записывается следующим образом:
x1(k+1) = c11x1(k) + c12x2(k) + ... + c1nxn(k) + d1
x2(k+1) = c21x1(k) + c22x2(k) + ... + c2nxn(k) + d2
...
xn(k+1) = cn1x1(k) + cn2x2(k) + ... + cnnxn(k) + dn
Таким образом i-тая компонента (k+1)-го приближения к решению вычисляется по формуле xi(k+1) = å nj=1 cijxj(k), i=1, ..., n. Имеет место следующая теорема:
ТЕОРЕМА. Для сходимости последовательных приближений {x(k)} метода простой итерации к точному решению системы (1.11) достаточно, чтобы || C || < 1.
Таким образом, если некоторая норма матрицы C меньше единицы, то итерационный процесс, основанный на формуле (1.13), гарантированно сходится к искомому решению при любом начальном приближении x(0).
Метод Жордана-Гауса
Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:
1. Проверяется, не является ли система несовместной.
2.Если система содержит противоречивое уравнение, то она несовместна
3. Проверяется возможность сокращения числа уравнений.
4. Если в системе содержится тривиальное уравнение, его вычеркивают.
5. Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
6. Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
Далее заново переходят к пункту 1.
Матричний метод
Матричний метод розв'язку систем лінійних алгебраїчних рівнянь з ненульовим визначником полягає в наступному.
Нехай дана система n лінійних рівнянь з n невідомими (над довільним полем):
Тоді її можна переписати в матричній формі , де A - основна матриця системи, і - стовпці вільних членів і рішень системи відповідно.
Помножимо це матричне рівняння ліворуч на A-1 - матрицю, зворотню до матриці A.
Оскільки A-1⋅A=E (враховуючи асоциативність матричного добутку), одержуємо рівняння, права частина якого дасть стовпець розв’язання вихідної системи. Умовою застосовності даного методу (як і взагалі існування розв'язку неоднорідної системи лінійних рівнянь із числом рівнянь, рівним числу невідомих) є невирідженість матриці A. Необхідною і достатньою умовою цього є нерівність нулю визначника матриці A.
